Discontinuity
A function that is not continuous at a point c of its domain is called discontinuous at c. Usually this concept of discontinuity is used also in a larger sense: if a point c is an accumulation point of the domain that does not belong to the domain, then the function is called discontinuous at c. For example the function f(x)=lnx is called discontinuous at zero. But pay attention because, as zero does not belong to the domain, it makes no sense to ask whether the functions is continuous or not at zero. So, strictly speaking, the function is neither continuous not discontinuous at zero: the word discontinuous is used here in a somewhat improper sense.
A function may be discontinuous at a point c (that belongs to the domain or is an accumulation point for the domain) for one of the following reasons:
-
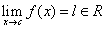 , but
l≠f(c). In this case the function
, but
l≠f(c). In this case the function
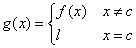 is almost the same than
f and is continuous at c: it is called
a continuous extension of f. The
discontinuity is removable.
is almost the same than
f and is continuous at c: it is called
a continuous extension of f. The
discontinuity is removable.
-
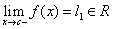 and
and
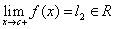 , but
l1≠l2. In this
case we'll say that function jumps between
l1 and l2 and
|l1-l2| is the height of
the jump.
, but
l1≠l2. In this
case we'll say that function jumps between
l1 and l2 and
|l1-l2| is the height of
the jump.
-
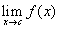 does
not exist or is infinite.
does
not exist or is infinite.
Examples
-
Consider the function
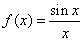 . As zero does
not belong to the domain but is an accumulation point for
the domain, the function is discontinuous at zero. The
function
. As zero does
not belong to the domain but is an accumulation point for
the domain, the function is discontinuous at zero. The
function 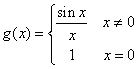 is continuous
everywhere and is a continuous extension of f.
is continuous
everywhere and is a continuous extension of f.
-
Consider the function
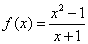 . As -1 does
not belong to the domain but is an accumulation point for
the domain, the function is discontinuous at -1. The
function g(x)=x-1 is a continuous extension of
f.
. As -1 does
not belong to the domain but is an accumulation point for
the domain, the function is discontinuous at -1. The
function g(x)=x-1 is a continuous extension of
f.
-
Consider the function f(x)=|sign(x)|. The function is not continuous at zero because
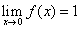 while f(0)=0. The
constant function f(x)=1 is a continuous
extension of f.
while f(0)=0. The
constant function f(x)=1 is a continuous
extension of f.
-
Consider the function f(x)=sign(x). As
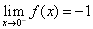 and
and
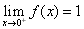 , the
function has a jump at zero with height two.
, the
function has a jump at zero with height two.
-
Consider the function
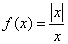 . As
. As 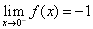 and
and 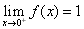 , the function has a jump at zero with
height two. Observe that, unlike the previous example,
zero does not belong to the domain.
, the function has a jump at zero with
height two. Observe that, unlike the previous example,
zero does not belong to the domain.
-
Consider the function
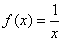 . As
. As 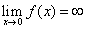 the function is
discontinuous at zero (observe that zero does not belong
to the domain of the function).
the function is
discontinuous at zero (observe that zero does not belong
to the domain of the function).
-
Consider the function
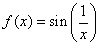 . As
. As 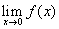 does not exist, the
function is discontinuous at zero.
does not exist, the
function is discontinuous at zero.