Examples and further techniques
Through the examples in this page we show some of the most common techniques used in the calculation of limits.
-
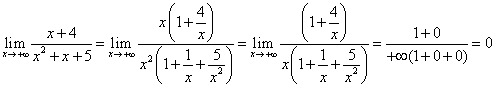 . Use this technique when
searching the limit of a rational function with
x→±∞.
. Use this technique when
searching the limit of a rational function with
x→±∞.
-
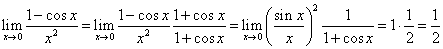 .
.
-
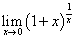 . Change the variable from
x to t=1/x. As x tends to zero,
t tends to infinity. Thus
. Change the variable from
x to t=1/x. As x tends to zero,
t tends to infinity. Thus 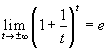 .
.
-
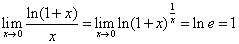 .
.
-
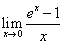 . Change the variable from
x to ex-1=t. As
x tends to zero, t tends also to zero.
The limit transforms in the reciprocal of limit 4:
. Change the variable from
x to ex-1=t. As
x tends to zero, t tends also to zero.
The limit transforms in the reciprocal of limit 4: 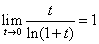 .
.
-
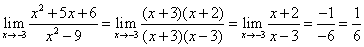 . This technique often works in
the case of a rational function in the form
0/0.
. This technique often works in
the case of a rational function in the form
0/0.
-
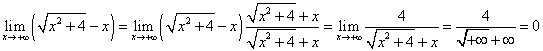 .
.
-
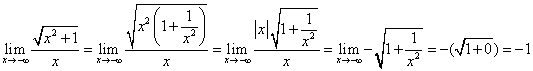 .
.
-
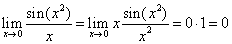 . Here we have implicitly used a
substitution x2=t. As x tends
to zero, also t tends to zero. We can treat many
other cases in the same way: usually the substitution will
not be written explicitly. See the following example.
. Here we have implicitly used a
substitution x2=t. As x tends
to zero, also t tends to zero. We can treat many
other cases in the same way: usually the substitution will
not be written explicitly. See the following example.
-
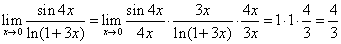 .
.