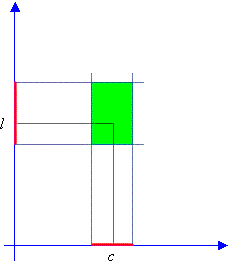
Two important theorems
First theorem: Uniqueness of the limit.
A function may have at most one limit as x approaches a given point c.
This theorem is very important and its proof can be deduced from the following picture, where we have used the usual reductio ad absurdum, by supposing the existence of two different limits for the function.
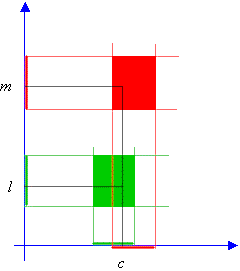
Second theorem: The sign theorem
A function that has a non zero limit has the same sign of the limit, near the point c.
The proof of this theorem is very easy and immediately follows by examining the following picture.