Exercises
1 - Evaluate the following limits:
-
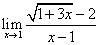. [Use the identity
(a-b)(a+b)=a2-b2].
-
.
-
.
-
.
-
.
-
.
-
.
-
.
-
.
-
.
-
.
-
.
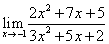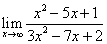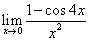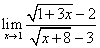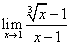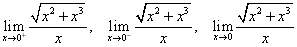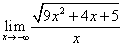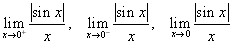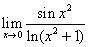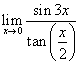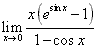2 - Use the squeezing principle to evaluate:
-
.
-
.
-
.
-
.
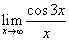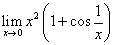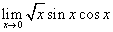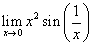3 - Suppose that 
. Prove that
.
4 - Prove, through an example, that if |f(x)|→l, f(x) may have no limit.
5 - Find a and b such that the function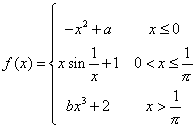 
is continuous everywhere.
6 - Find a and b such that the function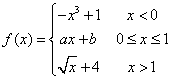 
is continuous everywhere.
7 - Suppose that the function f(x) is continuous in the compact interval [0,1], and that f(x) belongs to [0,1], for every x. Show that there exists c in [0,1] such that f(c)=c (c is called a fixed point).
8 - Show that at any given time there are always antipodal points on the earth's equator with the same temperature. [Show that for a function f(x) that is continuous in the compact interval [0,1], with f(0)=f(1), there exists a c such that f(c)=f(c+1/2].
9 - Consider the function f(x)=x2-2xsinx-1. Use the intermediate value theorem to prove that there exist two real numbers α<0 and β>0 such that f(α)=0 and f(β)=0.
10 - Prove that the equation ex=2-x has at least one real root.
11 - Prove that the equation ax3+bx2+cx+d=0 has at least one real root.
12 - Suppose that f(x) is a polynomial of even degree. Prove that the function has either a least or a greatest value, but not both.
13 - Suppose that f(x) is a polynomial of odd degree. Prove that the equation f(x)=a has at least one solution for every value of a.