A more formal definition
It turns out that, in order to give a formal definition of limit, it's better to begin investigation from the codomain instead of the domain.
More precisely, given an accumulation point c for the domain D of a function f, we said that the limit is the answer to the following question: what is the behaviour of f when x approaches c? Here the focus is on the variable x that "moves" towards c. In order to formalize this definition it turns out that we are forced to focus on the possible values of the function: given a number l, try to find the set A of all elements x of the domain whose images are close to l. If all the points sufficiently close to c belong to A, then l is the limit, otherwise it is not.
This requires a precise definition of what we mean by "close". For the purpose of our simplified theory of limits, this definition can be concentrated as follows:
- Given a real number c, we call neighbourhood of c an open interval containing c.
- An interval like ]c,+∞[ is a neighbourhood of +∞.
- An interval like ]-∞,c[ is a neighbourhood of -∞.
So, given a real number c and one of its neighbourhoods, say ]a,b[, every number belonging to ]a,b[ is close to c, other numbers are not close to c. The neighbourhood is a measure of "closeness": changing the neighbourhood affects the property of being close or not to c.
We can now give the formal definition of limit:
![]() Given a function
Given a function ![]() ,
and an accumulation point c for D (+∞
and -∞ are allowed), we say that l (+∞ and
-∞ are allowed also for l) is the limit of the
function as x tends to c, if for every
neighbourhood U of l we are able to find a
neighbourhood V of c such that the values of
the function f for all points x
,
and an accumulation point c for D (+∞
and -∞ are allowed), we say that l (+∞ and
-∞ are allowed also for l) is the limit of the
function as x tends to c, if for every
neighbourhood U of l we are able to find a
neighbourhood V of c such that the values of
the function f for all points x![]() V, c excepted, belong to U.
V, c excepted, belong to U.
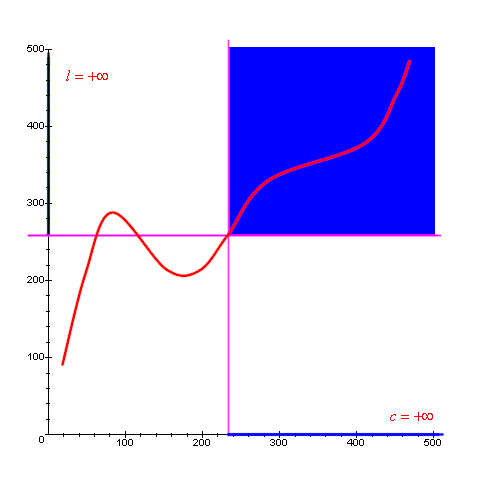
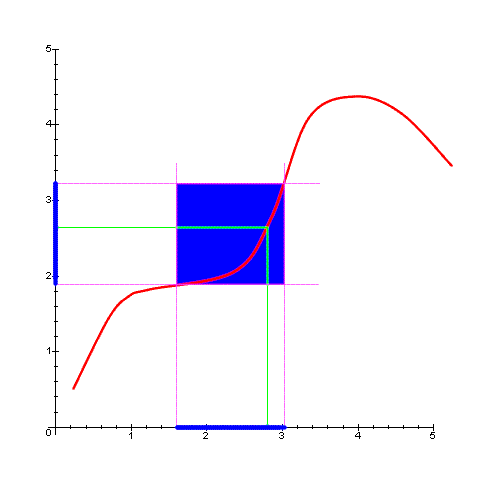
In the following picture you can see a graphical representation
of what happens when both c and l are numbers,
that is ![]() .
.
In the folllowing picture you can see a graphical representation
of what happens when c is a number and l is
+∞, that is ![]() .
.
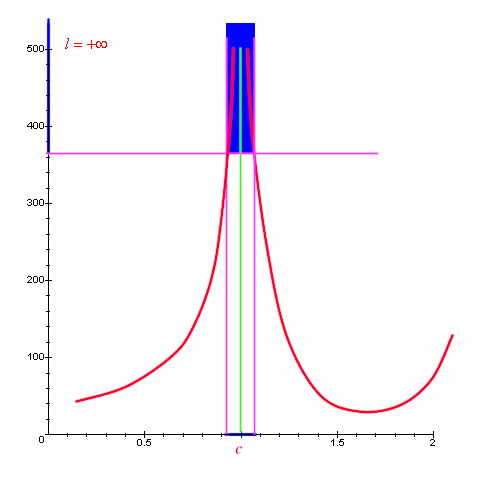
In the following picture you can see a graphical representation
of what happens when both c and l are
+∞, that is ![]() .
.