Introduction
Functions (from R to R)
Let D and C be subsets of
R. A function f
assigns elements from D to C. We write a
function: 
. D is called the
domain of f, C is called the
codomain. We'll use the traditional x for
the independent variable and y for the
dependent one. The variable x is often called
the argument. The number f(x) is called the
value of f at x, or the
image of x under f. We usually write
this in a concise form: 
. The range
of f is the subset, f(D), of C,
defined as follows: 
, that is the subset of
all elements of C that are the image of at least one
element of D.
In the following picture we have D={2,4,6,7}, C={1,3,5,8,9}, f(D)={3,5,8}. We also have, for example, f(2)=5, f(7)=8.
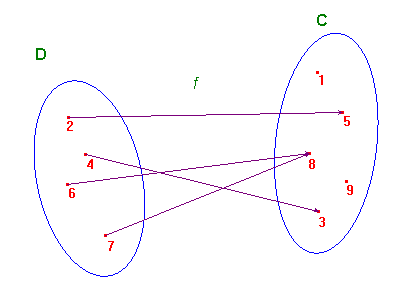
Observe that a function has only exactly one value for each x in D. In other words every element in D has only an arrow in his quiver that he is forced to shoot at some element in C; on the contrary not every element of C must be shot by some arrow, while some element may be shot by more than one!.
A function is called surjective or onto, if
f(D)=C.
A function is called injective if
f(x1)=f(x2) only when
x1=x2.
A function that is both surjective and injective is called
bijective or one-to-one.
If A is a subset of D we shall call f(A) the subset of all elements y of C such that y=f(x) for some x in A. In the same way we'll call f -1(B) the subset of all elements x of D for which f(x) is in B. f(A) is the image of A, f -1(B) is the inverse image of B.
Sometimes the domain and codomain of a function are not given (it's better to avoid doing this). In this case one assumes that the codomain is the whole set of real numbers, while the domain is the largest possible set of real numbers where the involved operations may be performed. This set is called the natural domain.
Functions defined in pieces
To construct functions from R to
R we may use the four operations
(addition, subtraction, multiplication, division) and other
elementary techniques (radicals, trigonometric functions,
logarithms, exponentials), but in the applications we usually
find functions defined in pieces, as in the following
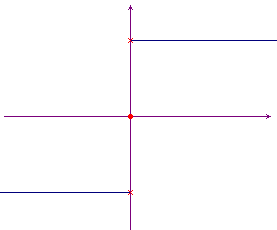
example: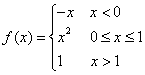 
. This is an important technique used
to construct non-elementary functions. We'll learn
other methods to construct non-elementary functions.
One of the most important functions defined in pieces is the
following: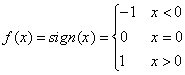 
. For every real number
x we can write x =
sign(x)×|x|.
The graph of a function f is the set: 
. This subset of the cartesian plane usually is a curve
in the ordinary sense (sometimes a curve that is a collection of
pieces of ordinary curves), with the important restriction that
a vertical line can intersect the graph in no more than one
point.
The two functions defined in pieces that we have just considered have the following graphs:
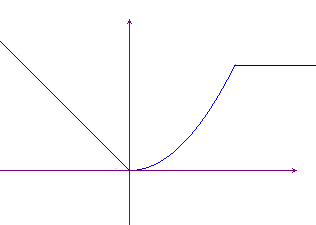
Interval notation
Some subsets of R deserve special attention: for them we'll use the following notations.
-
[a,b] = {x
R | a ≤ x ≤ b}
closed interval from a to b (a segment)
-
]a,b[ = {x
R | a < x <
b} open interval from a to b (a
segment)
-
[a,b[ = {x
R | a ≤ x <
b} interval from a to b, left
closed, right open (a segment)
-
]a,b] = {x
R | a < x ≤
b} interval from a to b, right
closed, left open (a segment)
-
[a,+∞[ = {x
R | x ≥a} (a
half-line)
-
]a,+∞[ = {x
R | x > a} (a
half-line)
-
]-∞,a] = {x
R | x ≤ a} (a
half-line)
-
]-∞,a[ = {x
R | x < a} (a
half-line)
- ]-∞,+∞[ = R (the whole line of real numbers)
Forming new functions out of old ones
In order to obtain new functions out of old ones the main techniques are the elementary ones based on addition, subtraction, multiplication, division; in addition we must consider function composition.
Sometimes the natural domains need to be changed.
The formal definitions are as follows:
- (f ± g)(x) = f(x) ± g(x)
- (fg)(x) = f(x)g(x)
- (f / g)(x) = f(x) / g(x)
- (f o g)(x) = f(g(x)).
If, for example, 
(with domain E =
[0,+∞[), and 
(with domain F =
]-∞,1]), then:
-
(f ± g)(x) =
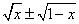, D = [0,1]
-
(fg)(x) =
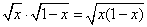, D = [0,1]
-
(f / g)(x) =
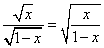, D = [0,1[
-
(g / f)(x) =
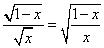, D =]0,1]
-
(f o g)(x) =
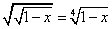, D = ]-∞,1]
-
(g o f)(x) =
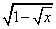, D = [0,1]
Note that (f / g)(x) ≠ (g / f)(x) (almost obvious), and (f o g)(x) ≠ (g o f)(x) (not so obvious!).
Note also that, while , in general
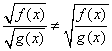: you can consider for example the case of
f(x)=x and g(x)=x-1.