The extended real line
For the purposes of limit theory it's useful to extend the set of real numbers with two other elements, that we write -∞ and +∞, and call, respectively, minus infinity, plus infinity. This extension is useful to treat functions or variables that grow without bounds. This extended set is called the extended real line. The usual order between "ordinary" real numbers is preserved and we define: -∞ < x < +∞, for all reals x. Sometimes we'll also use the symbol ∞, without any sign plus or minus, when it is unimportant to distinguish between the "+" and the "-".
Also the ordinary operations between numbers are extended, with some important exclusions, to this set, by means of the following definitions, where a is a real number, and A is a real number different from zero.
- a ± (+∞) = ±∞;
-
a ± (-∞) =
 ∞;
∞;
- (+∞) + (+∞) = +∞;
- (-∞) + (-∞) = -∞;
- A×(∞) = ∞ (with the usual sign rule);
- (∞)×(∞) = ∞ (with the usual sign rule);
-
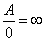 (with the usual sign rule; also 0
can have a sign in this context, as we'll see);
(with the usual sign rule; also 0
can have a sign in this context, as we'll see);
-
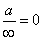 ;
;
-
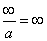 (with the usual sign rule).
(with the usual sign rule).
Observe that the following operations are not defined:
- (+∞) - (+∞); (-∞) + (+∞); (-∞) - (-∞); (+∞) + (-∞)
- 0×(∞)
-
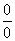
-
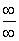
![]() Remember that +∞ and -∞
are not numbers: do not write x = ±∞, if
x is a number.
Remember that +∞ and -∞
are not numbers: do not write x = ±∞, if
x is a number.
It is also of the utmost importance to observe that the extended
real line, which we sometimes write ![]() , is not a set of
numbers in the ordinary sense. In fact the operations we have
introduced do not satisfy many of the usual properties. For
instance while the result of a+b changes if
you change either a or b, the operation
a+(+∞) has always the same result, no matter what
a is: 3+(+∞) = 4+(+∞) = (+∞)
+(+∞) = (+∞).
, is not a set of
numbers in the ordinary sense. In fact the operations we have
introduced do not satisfy many of the usual properties. For
instance while the result of a+b changes if
you change either a or b, the operation
a+(+∞) has always the same result, no matter what
a is: 3+(+∞) = 4+(+∞) = (+∞)
+(+∞) = (+∞).
Some examples
-
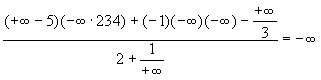 ;
;
-
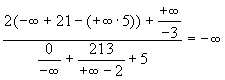 .
.