Simple applications

If we represent the vectors and points of ordinary three (or two) dimensional euclidean space as one column vectors (with three or two rows), and use the theory of matrices and determinants, some formulae of  ordinary analytic geometry are much more simple to remember.

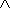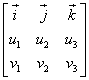• The vector product of two vectors: u=(u₁,u₂,u₃) and v=(v₁,v₂,v₃). The components of the vector w=uv are easily obtained calculating the "determinant" of  the matrix   by means of the cofactor expansion by row 1: .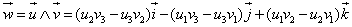

• Area of a triangle in a cartesian plane. Given a triangle whose vertices are A, B, C, the area of the triangle is obtained by the formula: 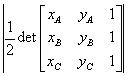. See the proof.

• As a consequence of  the previous formula you can easily deduce the condition under which three points belong to the same straight line: the triangle having the three points as vertices must have zero area.

• Area of a polygon in a cartesian plane. Given a polygon whose vertices are P₁, P₂, ..., Pn, the area is easily obtained by the formula: .
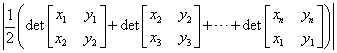