Vector spaces: just a quick look
In the set R2 one usually introduces two operations: the sum of two couples and the product of a couple by a number: (x1,x2)+(y1,y2)=(x 1+y1,x2+y2) and c(x1,x2)=(cx1,cx2). These operations turn the set of all couples of real numbers in a set that is almost identical to the set of ordinary vectors in the plane where the sum and multiplication by a number are defined in the usual geometric form.
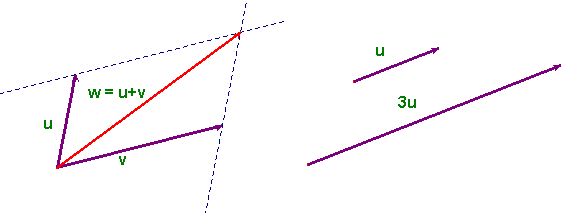
If we consider the set Rn of all n-tuples of real numbers (x1, x2, ..., xn) we can define sum and multiplication by a number in exactly the same way:
(x1, x2, ..., xn)+(y1, y2, ..., yn)=(x1+y1, x2+y2, ..., xn+yn) and c(x1, x2, ..., xn)=(cx1, cx2, ..., cxn).
These definitions turn the set Rn in a set where the operations just defined have all the usual properties of the operations between vectors (of course we can now give no geometric representation if n>3). We shall say that Rn, with these two operations is a vector space of dimension n. More general sets can be turned into vector spaces by suitable definitions of a sum and a product by a real number: these spaces play an important role in many applications of maths, but they are beyond the purpose of this brief introduction. It is usual to represent the elements of the vector space Rn as one column matrices.
We can now go one step further and introduce functions between
vector spaces: f :
Rn→Rm.
A function of this kind transforms a n-tuple in a
m-tuple. For example the function 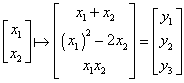 transforms each couple of real numbers in a tern of real
numbers, so it is a function f :
R2→R3.
transforms each couple of real numbers in a tern of real
numbers, so it is a function f :
R2→R3.
If we consider a function f : Rn→Rm, the elements of Rn are called independent variables, while the elements of Rm are called dependent variables (as usual with functions!).
The most important functions of this kind are the so called
linear functions: the only allowed operations on the
independent variables are sums between the variables and
multiplications by scalars. The function in the previous example
is not a linear function, while the following is: 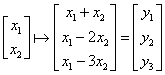 . If we remember matrix multiplication, it is easy to
show that this function can also be written as:
. If we remember matrix multiplication, it is easy to
show that this function can also be written as: 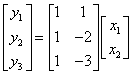 . This is the reason why we represent the elements of
Rn as one column matrices. We say
that the matrix
. This is the reason why we represent the elements of
Rn as one column matrices. We say
that the matrix 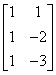 represents the function.
This fact is of a general nature:
represents the function.
This fact is of a general nature:
- Given any linear function f : Rn→Rm, there exists a unique m×n matrix A such that the image y in Rm of an element x of Rn through the function f may be obtained as y = Ax, where x and y are one column matrices.
- Given a generic m×n matrix A, the function y = f(x) = Ax is a linear function f : Rn→Rm.
In the special case where n=m=1 the function is simply f(x)=ax, where a is a real number, and the matrix A reduces to a single entry matrix: A=[a]. This function has a straight line through the origin as graph in a cartesian plane. This is the reason why these functions are called linear.
Using the terminology just introduced we can interpret the problem of solving a linear system of m equations in n unknowns, Ax = b, as the problem of finding the inverse image of an element b of Rm under the function represented by the matrix A:
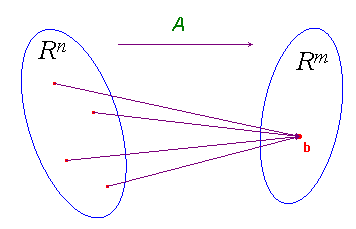
The theory we have developed proves that this inverse image can have no elements (inconsistent system), only one element, or infinitely many elements.