Cramer's rule
Consider a linear system of n equations in n unknowns, written in compact form: Ax = b. If the matrix A is non singular the system has a unique solution that can easily be expressed by: x = A-1b. This means that writing the solution of such a system is much like the case of a linear equation in one unknown.
A consequence of this observation is an important theorem, known as Cramer's rule, that, though not much used in practice, is very important from a theoretical point of view because it reveals explicitly how the solution depends on the coefficients of the augmented matrix.
Given a linear system of n equations in n unknowns, call Δ the determinant of the matrix A of the system, Δi the determinant of the matrix formed by replacing the i-th column of the matrix A by the constants b1, b2, ...,bn. Then if ≠0 the unique solution of the system is
.
Example
Solve the system Ax =
b where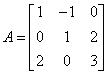 
and 
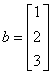. It's easy to find that
det(A)=-1. By Cramer's rule we have:
.
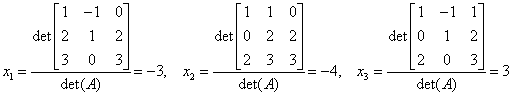We can easily check out the solution. We have: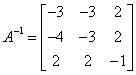 
. So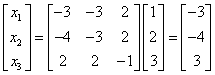 
.