Square matrices, determinants and inverses
Square matrices
A square matrix is a n×n matrix. The
common number n of rows and columns is also called the
order of the matrix. In the set of all matrices of
order n, matrix product is an internal operation and
the matrix whose entries are 
is called the identity matrix, In,
as it satisfies the following properties: for every given matrix
A, A·In=In·A=A. In
other words In is the neutral element for
matrix product.
In this space it is also possible to define the k-th power of a matrix: A0=In, An=A·An-1.
A square matrix A of order n, is called non-singular or invertible if there exists a matrix B of order n such that
A·B = B·A =In.
The matrix B, if it exists, is unique and is called the inverse of A and is denoted by A-1.
Example
Find the inverse, if it exists, of the matrix 
. We must search a matrix of the form 
such that the previous identity holds. This means we must solve
the following linear system in four unknowns: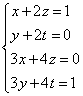 
. Via the Gauss-Jordan algorithm we easy find the
solution: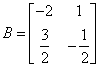 
.
The main properties of the inverse of a matrix are:
-
(A-1)-1 = A
-
(AB)-1 = B-1A-1
The problem of finding the inverse, if it exists, of a given matrix A, is very important. The technique we used in the previous example relates this problem to a question of solving a linear system. In some sense this is unsatisfactory, since it is not simple to solve such a system without a lot of work. So we now look for a different strategy.
First of all we try to generalize the previous example to a
generic matrix of order two: 
. We write down the system as in the example above
and obtain the following augmented matrix: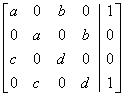 
.
-
If a=c=0, the system has no solution.
-
If a≠0, via the Gauss-Jordan algorithm we obtain the following reduced row-echelon form of the augmented matrix:
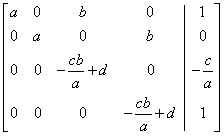. The system has one solution if (and only if)
ad-bc≠0, and the solution gives the
inverse matrix: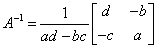 
.
-
If c≠0 and a=0 we can interchange rows one and two with rows three and four and obtain the same result.
So the number ad-bc plays a special role in the theory of matrices of order two: if it is not zero the matrix has an inverse, otherwise it has no inverse.
Determinants
Given a generic matrix of order two, ,
the number ad-bc is the determinant of the
matrix, det(A). The notation 
is
also used. If and only if det(A) is different from zero
the matrix has a unique inverse. If we attempt to repeat the
calculations above to matrices of order three, then it is very
likely that we shall end up in a mess with possibly no firm
conclusion. (Try it if you must!). We shall follow a different
approach: precisely an inductive one. In other words we shall
define the determinant of a matrix of order n in terms
of determinants of matrices of order n-1: as we know
the determinant of a matrix of order two this will lead us to
the desired result.
A new definition is needed in order to simplify the notations.
Given a matrix A of order n and an entry
aij we consider the new matrix,
Aij, of order n-1 that we obtain if
we delete the i-th row and j-th column
of A: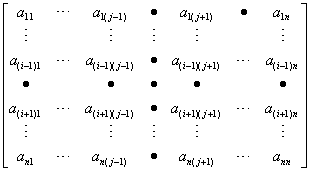 
. The number 
is called the cofactor of the entry
aij in the matrix A.
Given a row 
or a column 
one can prove (but it is not so easy!) that the
following expressions are equal and independent of the row or
column chosen: 
. These expression are
called cofactor expansions by row i or by column
j. The common value of these expressions is called the
determinant of the matrix A, denoted by
det(A).
It is easy to check that this agrees with our earlier definition of the determinant of a matrix of order two.
Example
Find the determinant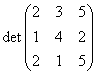 
. Let us use the
cofactor expansion by row 1. Then:
so that det(A) = 2·18+3·(-1)+5·(-7) = -2.
Calculating the inverse of a matrix
In order to outline a procedure for finding the inverse of a matrix we need two more definitions.
Given a matrix A we call transpose of A the
matrix the matrix, At, obtained by
interchanging the rows and columns of the matrix A. For
example if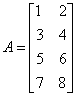 
, then 
. If X is a one column matrix (a column
vector),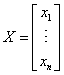 
, we have 
,
a property that will be useful in the following.
Given a matrix A the adjoint of A is the matrix, adj(A) is the transpose of the matrix of the cofactors of the entries of A.
Now it can be proved that a matrix
A is invertible if and only if det(A) is
different from zero and 
.
Example
Given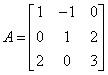 
, we have: 
.
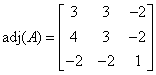As det(A)=-1, it follows that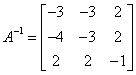 
.