www.batmath.it
Properties of determinants
Simple observations - Elementary row or column operations
- If a matrix has a zero row or column then its determinant is zero.
- If a matrix is triangular then the determinant is the product of the entries of the main diagonal.
Appropriate use of elementary row or column operations can strongly simplify the calculation of determinants, so we shall examine them with some detail.
- Interchanging two rows or columns of a matrix changes the sign of the determinant.
- Multiplying a row or a column by a non-zero constant c results in the multiplication of the determinant by the same value c.
- If a multiple of a row is added to another row the determinant does not change.
Example
Consider the matrix  . Adding -1 times row 4
to row 2 and, successively -2 times row 4 to row 3 we obtain:
. Adding -1 times row 4
to row 2 and, successively -2 times row 4 to row 3 we obtain:
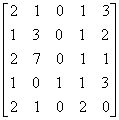 . Using cofactor expansion by column
3, we have: det(A) =
. Using cofactor expansion by column
3, we have: det(A) = 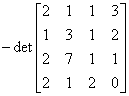 .
Now adding -1 times column 3 to column 1 and .1 times row 1 to
row 3, we have:
.
Now adding -1 times column 3 to column 1 and .1 times row 1 to
row 3, we have: 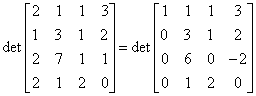 . So we obtain
. So we obtain 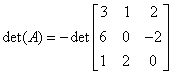 . Finally, adding 1 times row 1 to row 2 we find:
. Finally, adding 1 times row 1 to row 2 we find:
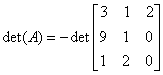 . We can easily conclude that
det(A)=-34.
. We can easily conclude that
det(A)=-34.
Other properties of determinants
- det(A) = det(At)
- det(AB) = det(A)det(B)
-
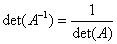 .
.
copyright 2000 et seq. maddalena falanga & luciano battaia
first published on march 15 2002 - last updated on september 01
2003