Introduction
The simplest linear (i.e. first degree) equation is an equation
in one unknown: ax=b. Solving this equation is very
simple: as the coefficient a must be non zero
(otherwise the equation is not a first degree one), we
immediately obtain ![]() .
.
From a geometrical point of view this may be interpreted as follows: in a cartesian coordinate system draw the lines y=ax and y=b. The unique solution of the equation is the first coordinate of the intersection point of these two straight lines: there must be an intersection point since a≠0 means, geometrically, that the line y=ax is not horizontal, that is not parallel to the line y=b.
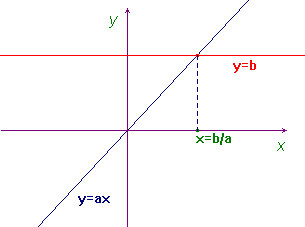
The main reason for naming this equation linear is just the fact that in this simple case the graph of y=ax is a straight line.
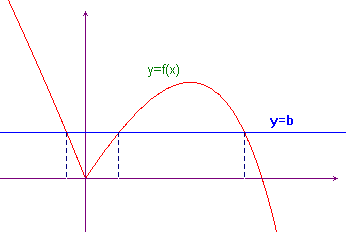
In fact the most general equation in one unknown has a form like this: f(x)=b. If we represent in a cartesian coordinate system the function y=f(x) and the straight line y=b, the solutions of the equation are simply the first coordinate (x) of the points of intersection between the graph of f(x) and the straight line. In the following picture there are three intersections and so the corresponding equation has three solutions.
Now let's consider a system of two equations in one unknown,
that we shall write in the usual form: ![]() .
To solve this system means to find the real numbers
that satisfy both the first and the second equation, in other
words the intersection of the sets that contain the solutions of
the two equations. As these sets contain exactly one number,
it's very difficult to find something in common between
them: this problem is somewhat uninteresting.
.
To solve this system means to find the real numbers
that satisfy both the first and the second equation, in other
words the intersection of the sets that contain the solutions of
the two equations. As these sets contain exactly one number,
it's very difficult to find something in common between
them: this problem is somewhat uninteresting.
So let's go one step further and consider a linear equation in two unknowns: ax+by=c. This equation has always infinitely many solutions (if we exclude the trivial and uninteresting case when both a and b are zero). From a geometrical point of view the set that contains all the solutions of this equation may be represented as a line in a plane were we have introduced a cartesian coordinate system Oxy.
If we go still further we may say that a linear equation in three unknowns has infinitely many solutions that we can represent as a plane in tridimensional space with a cartesian coordinate system Oxyz. So:
- An equation in one unknown, ax=b, is a point in the straight line (with a cartesian coordinate system Ox).
- An equation in two unknowns, ax+by=c, is a line in the plane (with a cartesian coordinate system Oxy).
- An equation in three unknowns, ax+by+cz=d, is a plane in the space (with a cartesian coordinate system Oxyz).
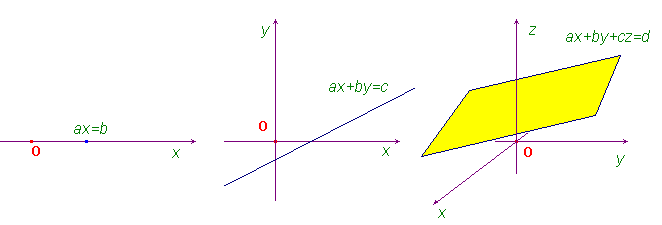
What about an equation in four unknowns? We shall say that its set of solutions, from a geometrical point of view, is a hyperplane in a four dimensional space (that obviously we can't picture in a traditional way).
The important difference between an equation in one or more unknowns is in the cardinality of the set of solutions: all equations in at least two unknowns have infinitely many solutions. This means that solving a system of equations in more than one unknown is not a trivial problem. The geometric representation is very useful to full understand the problem. For example it's easy to conclude that:
- A system of two equations in two unknowns may have one solution (straight lines intersecting in one point), no solution (parallel straight lines) or infinitely many solutions (two overlapping lines).
- A system of three equations in two unknowns, although it may have one or even infinitely many solutions, usually has no solution because three straight lines in a plane, in general, have no common point.
- A system of two equations in three unknowns may have no solution (parallel planes), or infinitely many solutions (planes having a line in common or completely overlapping).
- A system of three equations in three unknowns may have no solution (at least two of the planes are parallel), infinitely many solutions (planes belonging to a sheaf), or one solution (planes having only one common point).
- A system of more than three equations in three unknowns usually has no solution, because four or more planes in space normally fail to have something in common.
Examples:
-
The system
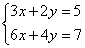 has no solution
(parallel lines - try to draw them!).
has no solution
(parallel lines - try to draw them!).
-
The system
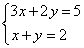 has exactly one
solution, that is the point of intersection of the two lines:
(1,1).
has exactly one
solution, that is the point of intersection of the two lines:
(1,1).
-
The system
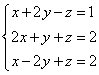 has exactly one
solution, the common point of the three planes:
has exactly one
solution, the common point of the three planes: 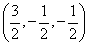 .
.
-
The system
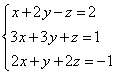 has infinitely many
solutions, as the planes belong to a sheaf.
has infinitely many
solutions, as the planes belong to a sheaf.
In the following we'll need systems of many equations (we'll say m equations) in many unknowns (we'll say n unknowns), so we shall use a more general notation:
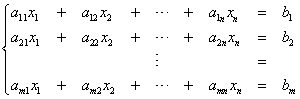 .
.
One of the problems of linear algebra is to find a general method of solution of such a system. This search will conduct us to a new mathematical theory, linear algebra, that has applications in many varied fields.