www.batmath.it

Matrices and operations between matrices

Preliminary definitions

A rectangular array of real numbers of the form 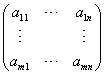, is called an m×n matrix on the field R, or simply an mn matrix on the field R, with m rows and n columns. Unless otherwise specified we'll use only real numbers, so we'll omit the specification "on the field R".  We count rows from the top and columns from the left. Hence represents the i-th row, while represents the j-th column. The number is the entry in the matrix on the i-th row and j-th column.

    Sometimes square brackets, [], are used in the place of parenthesis: .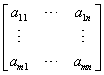 

     We'll denote by 0_mn , or simply by 0 when no confusion is possible, the mn matrix whose all entries are zero, and call this the zero-matrix or null-matrix.

See an example

Matrix addition

     Given two mn matrices 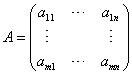,  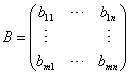, we write 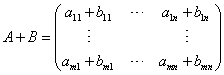, and call this the sum of the two matrices A and B.

     It is easy to proove that this operation between mn matrices obeys the following properties:

1. A+B = B+A (Commutative law)

2. A+(B+C) = (A+B)+C  (Associative law)

3. A+0_mn = A (Existence of a neutral element)

4. For every matrix A there exists a matrix A' such that A+A' = 0_mn  (Existence of an inverse)

The proof is an easy consequence of the same properties of ordinary addition, as matrix addition is simply entry-wise addition. In particular the matrix A' is the matrix obtained from A by multiplying each entry of A by -1, and we'll call it -A.

     As a consequence of these properties this composition law turns the set of all mn matrices into a commutative group.

Multiplication by a scalar

    Given the mn matrix 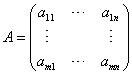and the real number c, we write 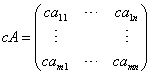and call this the product of the matrix A by the scalar c.

It is easy to proove that this operation obeys the following properties:

1. c(A + B) = cA + cB
2. (c + d)A = cA + dA
3. c(dA) = (cd)A
4. 0A = 0_mn
5. 1A = A
6. 

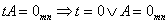
The proof is an easy consequence of ordinary multiplication, as multiplication by scalar is simply entry-wise multiplication by the number c.

As a consequence of these properties the set of all mn matrices, with the two operations just introduced, turns into a vector space (over the field R).

Matrix multiplication

     The question of multiplication of two matrices is rather more complicated. One could define matrix product simply by entry-wise multiplication, as in  matrix addition: this would lead to a product that has many of the usual properties of a product (commutative, associative, existence of a neutral element), but, for example, a matrix with only one zero entry would not have an inverse. Most of all, however, the main difficulty of such a definition concerns the developments of matrix theory: in fact matrices will be used to define special functions between multidimensional spaces (linear maps) and it's useful to introduce matrix multiplication in order to have a correspondence between this operation and the composition of functions.

     With this in mind we'll define matrix multiplication in a rather different way: a row by column multiplication. Given an mn matrix A and an np matrix B (observe that A has n columns, while B has n rows), the product matrix C will be a mp matrix whose entry c_ij is obtained as follows: choose the i-th row of the matrix A (that has n columns) and the j-th column of the matrix B (that has n rows), multiply each entry in the row by the corresponding entry in the column and sum up. Formally this can be written in the following way:

.

See some example

As you must have seen in the examples, matrix product doesn't always obey the commutative law: in fact in general it is not even possible to change the order in the product, due to the condition that the number of columns of the first matrix must equal the number of rows of the second one. Apart from this property, however, this product obeys many of the familiar laws of ordinary multiplication:

1. (AB)C = A(BC)  (associative law)
2. A(B+C) = AB + AC (first distributive law)
3. (A+B)C = AC + BC (second distributive law)
4. c(AB) = (cA)B = A(cB)

We do not give the proof of these laws; in the exercises you can check there validity in simple cases.

Matrix and augmented matrix of a linear system

     Given a linear system 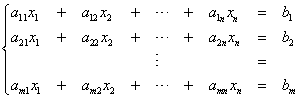, the matrices 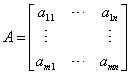and 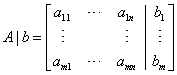will be called the matrix and the augmented matrix of the system. The notation A|b is used for the augmented matrix because the last column in the right (the column of constants) has a special significance in the resolution of linear systems.

If we consider the one-column matrices b = (matrix of the constants) and x = (matrix of the unknowns), a system of linear equations may be written in the compact form: Ax = b. This form is similar to the usual form of an equation of first degree in one unknown.

copyright 2000 et seq. maddalena falanga & luciano battaia

first published on march 15 2002 - last updated on september 01 2003