www.batmath.it

Relativity and the electromagnetic field

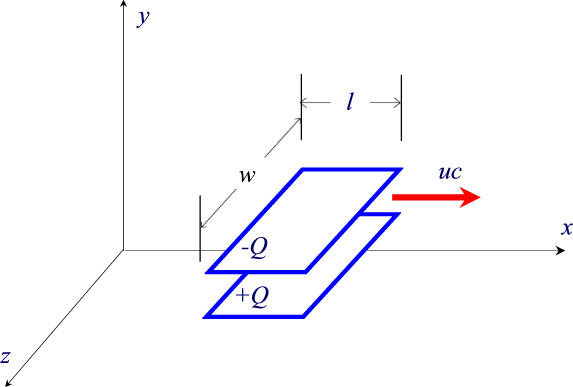
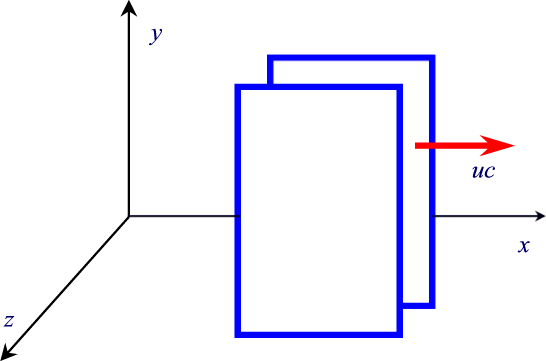
Let us consider, in a given system of reference, a flat capacitor, moving with speed v. Let l₀ and w₀ be its dimensions, measured by an observer at rest from the capacitor point of view. We shall put, for a reason of simplicity, u=v/c (this means that the speed is measured in "c units"); so we have v=uc. The dimensions, measured by an observer that is at rest with respect to the frame of reference, are  and w=w₀. Let us suppose the two plates charged, as in the picture above. Between the plates there is an electric field; it is uniform and points towards the positive y axis. Its value is given by the following formulas: .

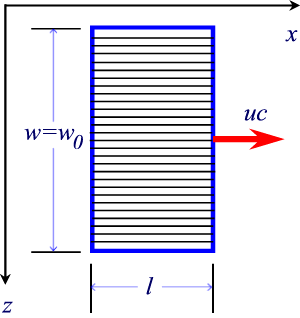
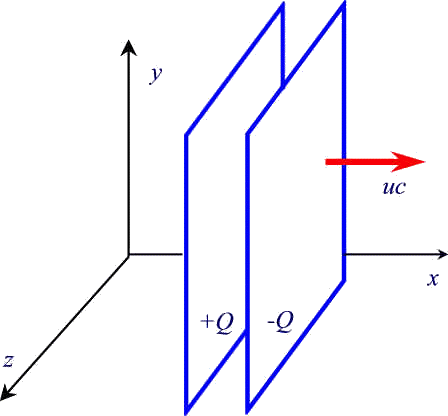
The two moving plates can be considered as electric currents and therefore they produce a magnetic field. If we suppose to divide each plate in many tight strips parallel to the direction of the movement, as shown in the picture here on the right, where the capacitor  is viewed from above, we can imagine both the plates as a set of wires carrying rectilinear currents.

If the subdivisions, that is the number of wires,  are in number of N, the negative plate will be filled by currents towards the negative direction of the x-axis, while the positive one will be filled by currents in the positive direction of the same axis.

The capacitor can be considered as a solenoid if we assume that every wire on the negative plate joins the correspondent on the positive plate, in order to lead to a closed circuit.

As in a normal solenoid, there will be a uniform magnetic field inside, directed towards the positive z-axis, and given by the following formulas (n is, as usual, the number of coils per unit length):

.

To find the current i we can use the following argument: the charge Q, on each plate, moves the length l towards the positive direction of the x-axis, in a time . The charge, q, on each subdivision is , so the current i is given by. For the field B we have, considering also that  w=w₀:  .

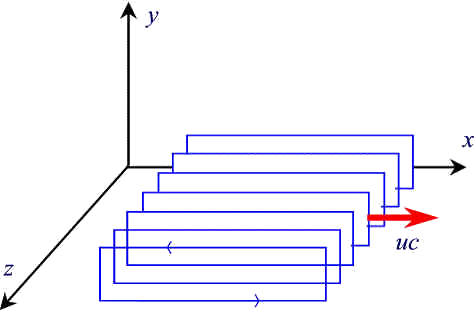
Now let us suppose we have a second frame of reference moving towards the positive direction of the x-axis, with speed V. Then, in  this frame of reference, the capacitor will have a different speed, v', and, if we put  and  , for the electric and magnetic field measured by the new observer, the same formulas we have obtained before will still be valid, with the simple replacement of u' for u:

 .

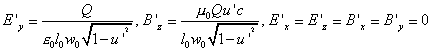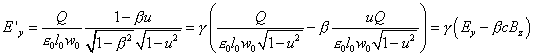Now we can use the formula for the addition of speed; if we divide both members by c, we obtain . Replacing this formula in the one that gives  E' and B', remembering that , we obtain: . In the same way, considering B'_z, we obtain .

If we consider again the capacitor, but now moving as in the following picture , we will find the same results as before, but now concerning the field's components E_z and B_y. We find, in a similar way: .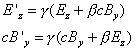

 

If the capacitor is placed as in the following figure, we find that  E_x=E'_x. We can easily understand that the electric field is the same for the two observers because the only thing that changes if viewed by the new observer is the distance between the plates, but the electric field of a capacitor doesn't depend on the distance between the plates.

It is not easy to prove that, for the magnetic field, the link B_x=B'_x is true when we change the frame of reference, in spite of the apparent simplicity of the formula, and we give up the calculations. Summarizing the formulas we have found we can write:

.

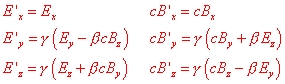It is necessary to underline that all what we have said in order to obtain these formulas is not a strict proof: these reasonings are rather an explanation of the role played by the Lorent transformations in the change of the electromagnetic field from an observer to another.

What is important in these formulas is the fact that they mix the fields: it makes no sense to speak about the electric or the magnetic field, even if we consider a case where the induction phenomenon or the shifting currents don't take part in, because the only important thing is the electromagnetic field. If, for example, we have a charge in quietness, in the first frame of reference we have the electric field of Coulomb's law and no magnetic field. In the second frame of reference we'll have an electric field  , not much different from the previous one, at least for low speed, but we'll have also a magnetic field, , small with small speed when γ1  and β0, but different from zero. Naturally this was already known in classical theory, because a charge in motion produces a magnetic field, but its presence can now be considered as a simple proof that electric and magnetic fields are the expression of just one physic event: the electromagnetic field. Measuring one field or the other is only a matter of frame of reference. The deep unification of these two concepts is one of the most important concepts of the theory of relativity, that really is characterized by a lot of unifications (space and time, energy and momentum, electric and magnetic fields).

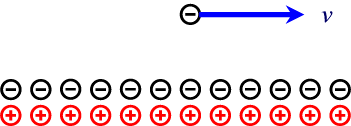
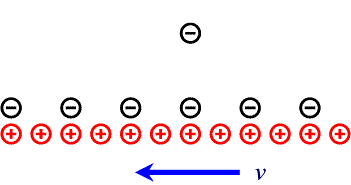
It is now easy to solve a famous paradox of the classical theory of magnetic interactions.

Let's consider a wire carrying a current i, as in the following picture and let's place a negative charge q, at a given distance from the wire, and moving, with respect to the wire, with the same speed v of the electrons of conduction in the wire (usually about 10^-4 m/s). In the frame of the wire a force, the force of Lorentz, will  influence the charge, brignign it nearer to the wire.In  the frame of the charge, from the calssical point of view, nothing changes for the magnetic field (we have positive charges moving "to the left" instead of negative ones moving "to the right", so the same current as before), but now the charge is at rest and so ther will be no magnetic effects. The charge is no more attracted towards the wire (observe that the speed we are considering is very low).

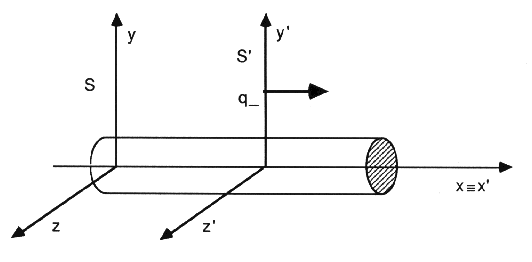
If we describe the experiment in terms of the formulas of the electromganeic field transformations, we will find that, in the reference of the wire, the charge feels the effect of a magnetic field, which has only a  B_z component coming out from the known expression of the field of a straight wire carrying a current. In the reference of the charge the charge itself will feel (besides the magnetic field similar to the previous one) also the effect of an electric field given by the formula and directed towards the positive y-axis. This electric fiield attracts the charge towards the wire. (The fact that the charge comes closer to the wire has to be an invariant property, independent from the frame of reference).

We can realize what we have just observed by a reasoning only based  on length measures. In the frame of the wire the positive and negative charges exactly balance because they are distributed in the same way (a wire carrying current does not produce electrostatic effects); in the frame of the charge positive charges are seen moving to the left, so they will be distributed on a shorter lenght and they will not balance negative charges.

copyright 2000 et seq. maddalena falanga & luciano battaia

first published on march 11 2002 - last updated on september 01 2003