The postulates of relativity
The special theory of relativity is based on the following postulates, the first of which (the Postulate of Relativity) is a generalisation of the Galilean principle of relativity to all phenomena, while the second directly assumes the results of Michelson and Morley's experiment.
- The laws of physics have always the same form in any inertial system.
- The velocity of light is a universal constant regardless of the motion of both the source and the observer (it's obvious that we consider the case of rectilinear and uniform motion).
It's worth remembering that, historically, the influence of Michelson and Morley's experiment on the formulation of the theory of relativity was, all in all, quite marginal, while the study of the problems connected with the Lorentz force on an electric charge in motion had greater importance.
The first of the postulates written above is an extension, and not the refusal, of the Galilean principle of relativity, the second replaces the absolute time of classical physic with an absolute speed, the velocity of light.
As a first consequence of these two postulates, although with a qualitative treatment, we want to deduce the formulas that link the co-ordinates of two phenomena seen from two different reference frames that move in rectilinear uniform motion one compared with the other.
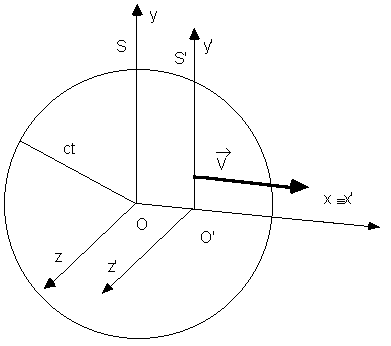
Let's consider a light source placed in the origin of a reference frame S (see the picture below). The two reference frames must coincide at the starting time. S and S' have to be equipped with 2 clocks, previously sinchronized, for example putting t'=0 when t=0. At this moment the source in O sends a light wave. After a certain time t, the wavefront seen by S is a spherical surface with the centre in O and ray r=ct, being c the wave velocity. The equation of this surface is: x2+y2+z2=c2t2. As a consequence of the principle of relativity, also S' must see the wavefront as a sphere: otherwise S' could understand that it is moving in comparison with S from the different shape of the wavefront (it's important to underline that we consider a situation without the presence of a propagation means: a similar reasoning isn't accettable for acustic or mechanical waves). Now the coordinates are x', y', z' and the time is t' (that could be different from t). But the velocity must be the same (second postulate of relativity). The wavefront seen by S' must have the equation x'2+y'2+z'2=c2t' 2.
If we replace in this equation the Galilean transformation, we'll obtain x2-2xVt+V2t2+y2+z 2=c2t2 that doesn't agree with the equation seen by S. We have to look for a transformation that can eliminate the unwanted terms. We need only to change the terms in x and t. Let's try with a transformation of the following kind: x'=x-Vt, y'=y, z'=z, t'=t+αx with α to be determined. (This choice is made because the transformation that we are looking for must be similar to the Galilean one and must be simple as well.) If we try to substitute the expressions, we find out: x2-2xVt+V2t2+y2+z 2=c2t2+2c2αtx+c 2α2x2.
The terms in xt can be eliminated considering 
and if we write 
, we obtain:
x2(1-β2)+y2+z2=c
2t2(1-β2) that presents some
other unwanted coefficients. If we finally put 
, then the formulas
become:
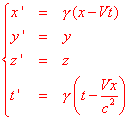
And in this way everything works, because, with this coordinate change, the equation comes down to the other one. This transformation is the only one that can solve all our problems. It takes the place of the Galilean one and it is called Lorentz transformation because Lorentz first found it, with the only request that the Maxwell's equations don't change. You can see that, in this Lorentz transformation, the first and the last line are almost symmetrical.
The usual differentiation allows us to write the formulas for the composition of the velocity:
.
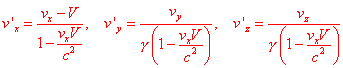It is interesting to see how this formulas work with some examples. What is important for us is their fundamental consequence: by adding velocities lower than the speed of light you will still obtain velocities lower than the speed of light.