Galilean relativity and Galileo's transformations
The principle of Galilean relativity asserts that all the inertial systems of reference are physically equivalent: no experiment performed inside a given system of reference can highlight the rectilinear and uniform motion of the same system, or, in other words, the physical laws found by experimenters who work in laboratories in relative rectilinear and uniform motion must have the same shape. Now we must deduce the formulas that link the time-space coordinates of an event seen from two different observers and show that the laws of physics are invariant in the passage from one frame of reference to another (in shape): in short we must translate into formulas the content of this principle.
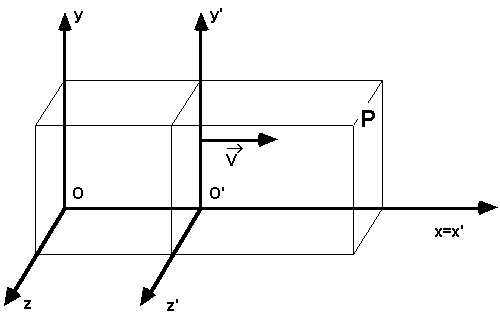
Let us consider two frames of reference, S and S’. We
suppose that S’is moving, with respect to S, in a
rectilinear and uniform motion, with speed 
. Let us suppose that the
observers S and S’ have two clocks to measure times,
previously synchronised in such a way, for example, that,
when O is upon O’, both clocks point to zero.
It is not limiting to suppose, as we will do, the x axes of the
two systems of reference one upon the other, so as to have parallel to the same x
axis. Let us consider a certain physical event that happens in a
point P with co-ordinates (x, y, z) and (x’, y’,
z’) with respect to S and S’ and at times t and
t’ measured by the two observers.
Remembering that OO’ = vt and that it seems obvious to suppose t=t’, from the picture by side it follows immediately the validity of the:
Galilean Transformations: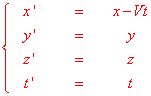 
We observe in particular that the fourth of these formulas has always been considered as obvious and it still is in everyday life. The refusal of the hypothesis (because this is an hypothesis and not a law proved by way of experiments) that the watches of the two observers should mark the same time is, as we will see, one of the innovative aspects of Einstein relativity.
With a first differentiation we can obtain the formulas for the
composition of speeds: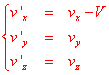
With another differentiation we can arrive to the fundamental
conclusion that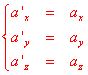 
If we consider the fact that the mass of bodies is an
unchangeable characteristic, using the definition of force, that
is the principal equation of dynamics, 
, we will conclude that the
form of the equations is indipendent from the reference system.
If we want to preserve the principle of relativity, an
alteration to Galileo's transformations must give rise to a
necessary modification of the principle of dynamics. This change
in the fundamental law of dynamics is one of the main outcomes
of the theory of relativity. It's important to point out
that Einstein's special theory of relaivity has not denied
the validity of Galileo's relativity, but only of the
mathematical formulas used in the passage from a given system of
reference to another: on tne contrary the validity of the
principle has been extended to all phenomena and not only to
mechanical ones.