Maxwell's equations and the ether
Maxwell's discovery of the general equations of the electromagnetism and all the consequences caused by them mark, historically, the beginning of a series of experiments, theories, discoveries which will finally lead Einstein, in 1905, to the formulation of the theory of relativity, with an article in Annalen der Physik ,volume 17: Zur Elektrodynamic bewegeter Korper (On the Electrodynamycs of the Bodies in Movement).
The first publication in complete form of the equations universally know as Equations of Maxwell is in 1873, in the work Electricity and Magnetism. It is significant, with regard to the importance of these equations, what Richard Feynmann writes in his The Feynmann lectures on Physics: "From a long view of the history of mankind - seen from, say, ten thousand years from now - there can be no doubt that the most significant event of the 19th century will be judged as Maxwell's disocvery of the laws of electrodynamics. The American Civil War will pale into provincial insignificance in comparison with this important scientific event of the same decade". (Vol.II, 1-6).
There is another important observation contained in the first chapter of the second volume of the aforementioned Feyman's book. This observation seems very interesting to us, but to completely understand it we must wait the introduction of the relativistic correction factors of the equations of motion. We may summarize Feynman's considerations as follows: the relativity is an aboslute necessity for the electromagnetic phenomena, independently from the speed at which we work. It is, maybe, possible to study a mechanics "of low velocities" and of the "ordinary space-time dimensions" as an approximation of a general theory. This approximation is technically much simpler than the general theory, and is in accordance, with a high degree of precision, with experimimental results in the great majority of the "concrete cases". In the electromagnetism that is not at all possible, because the relativistic corrections are the bases of the electromagnetic phenomena.
Maxwell's equations can be written, in an integral form, in the following way:
.
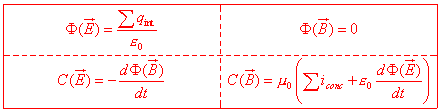The fundamental equation 
must be added to these equations, in order
to know how the electromagnetic field acts on the charges.
A fundamental consequence of these equations is the prevision,
only on the a theoretical basis, of the existence of
electromagnetic waves, that propagate with the speed 
. This merely theoretic prevision was
confirmed by a series of famous experiments by H. Hertz, in the
years 1886-89, therefore several years after the publication of
Maxwell's work. These equations, born for mathematical
requirements, foresaw phenomena which had an experimental
foundation. The publication of these equations gave rise to many
problems for the physicists of the second half of the nineteenth
century.
First a main consequance of the equations, as already mentioned, was the existence of waves, which are propagated with the same speed of the already well-known speed of light, without requiring any medium as a support: this was in contrast with the behavoiur of the acoustic waves that require a medium as support in order to propagate in space; moreover, and even worse, the equations weren't invariant under a Galilean transformation; finally there was no specification of the frame of reference in which the foreseen speed of these waves should be measured.
To try to solve these problems the concept of "ether", already used for the light waves, was introduced also for the just discovered electromagnetic waves. The ether was a substance that filled the whole universe, included the outer space, and served as support for the propagation of these waves. The speed c was the speed of the waves in the ether and Maxwell's equations were correct only with reference to the ether. This substance had to be very rigid to allow such high speeds of propagation (it is known that the acoustic waves travel with greater speed in more rigid substances), but at the same time it did not have to be very dense, otherwise the influence on the motion of the stars and the planets would have been too great. Despite this contradiction at the very beginning of the concept of ether, the idea of was very "hard to die".