Maxwell's equations
The four Maxwell's equations represent the analytic expression of the fundamental properties of the electromagnetic field. The physical meaning of the equations is summarized as follows:
|
|
This equation, which mathematically expresses Gauss's Theorem for the electric field, is substantially another way of writing Coulomb's law, and specifies the way by which charges interact. |
|
|
This equation, which mathematically expresses Gauss's Theorem for the magnetic field, turns into formulas the fundamental fact that an isolate magnetic monopole cannot be obtained. |
|
|
This equation is nothing more than the integral expression of Faraday-Neumann-Lenz's equation about induced electromotive forces. |
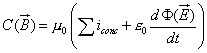
|
This equation (by far the most important one, especially for the birth of relativity), substantially expresses Ampère's theorem of circuitation, that is the law that explains the interaction between wires carrying currents, including a term about the so-called shift-current. It is, in the case of the magnetic field, the parallel of the equation for the flux of the electric field, that is, it can be assumed as a fundamental experimental law. It was obtained by Maxwell with simple mathematical considerations, in order to "save" Ampère's theorem of circulation. |
It must be observed that these equations do not give the values of E and B in every point of the space, if the charge and the currents are known, but global relationships only, concerning closed surfaces the first two, closed lines for the last two. Starting with these equations the explicit calculation of the fields is not easy to do, because it requires the use of some sophisticated mathematical techniques; they can easily be solved only in some cases of high symmetry.