The integral of f(x)=x2.
Given a natural number n>0, consider the following
dissection of the interval [0,2]: 
.
Using the infimum and the supremum of
f(x)=x2 in the intervals of the dissection,
we now define these step functions: 
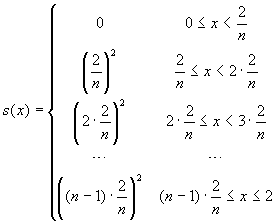, and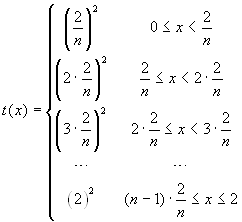 
, whose graphs are here
below.
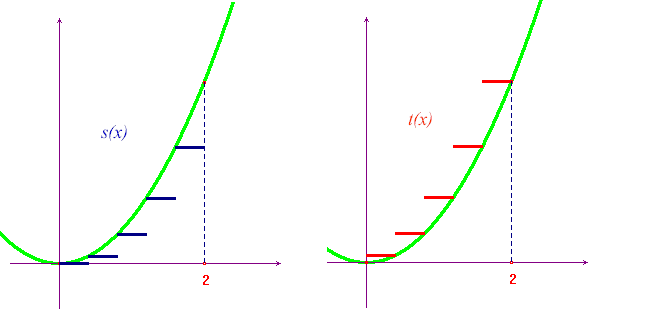
Let's now calculate their integrals. We need the formula
. You can find a proof of
this formula (in Italian). Then:
;
.
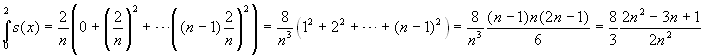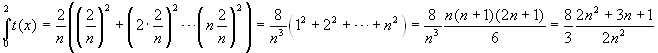If n gets greater and greater these two step functions
become closer and closer to f(x)=x2, and
their integrals tend to the common value 8/3. It's almost
obvious that 8/3 is the supremum of the integrals of all lower
step approximations of f, and, at the same time, the
infimum of the integrals of all upper step approximations of
f. So the function is Riemann integrable and 
.
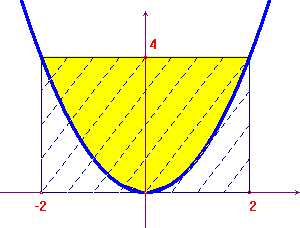
One can also obtain this result by means of the well known
Archimede's formula of the area of the parabolic
sector. The area of the outlined rectangle is 16, so the area of
the parabolic sector is 
and the area between
the function and the x-axis is 
.
This means that the area involved in our integral is exactly
8/3.
As you have seen in this page, the calculations involved are not easy, even if the function is a very simple one. Mathematicians have the stomach to do this kind of arithmetic, but they are also lazy enough to desire a theory to speed up calculations. This is the goal of the fundamental theorem of calculus.