Formal definition
Given two real numbers a<b, let us consider a
general function 
. If the function is
bounded we may always find two step functions s and
t such that s(x) ≤ f(x) ≤
t(x) for all x in [a,b]. These
functions may be considered as step approximations of
the function f : s is called a lower
approximation, t an upper
approximation.
Using the comparison property we conclude that 
.
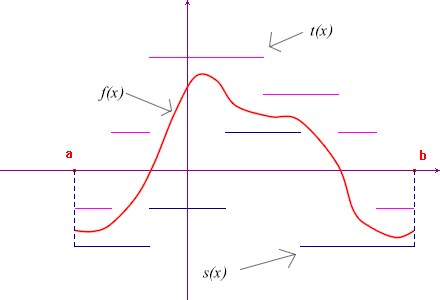
Let us now consider all the lower and upper approximations of f and the sets of their integrals:
, 
.
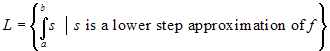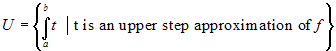L is certainly upper bounded and U is certainly lower bounded. With this in mind we give the following definitions:
I*(f) =
sup(L) is the lower Riemann integral of
f over the interval [a,b]
I*(f) =
inf(U) is the upper Riemann integral of
f over the interval [a,b]
If the lower and upper integrals are equal, the
function is called Riemann integrable and the
common value of
I*(f) and I*(f) is
called the Riemann integral of f over
the interval [a,b] and is denoted by
The following expressions are in use:
- The function f is called the integrand.
- The numbers a and b are called the bounds of integration.
- The domain [a,b] of the function is called the interval of integration.
Observe that if the function f is not bounded there may be no lower or upper step approximations of f: only bounded functions may be Riemann integrable.
Examples
Prove that f(x) = x is Riemann integrable
over [0,2] and calculate 
. Show that the
result is the same you can obtain by elementary geometric
methods. 
Prove that 
is Riemann
integrable over [0,2] and calculate 
.
Prove that 
(Dirichlet's function or characteristic
function of rationals) is not Riemann integrable over an
interval [a,b].
Observations
The previous examples show that there exist integrable and not integrable functions; they also show that the calculations needed to prove integrability and to calculate integrals are not simple at all.
Two problems now arise:
- What kind of functions are Riemann integrable?
- If a function is integrable, does there exist a technique, other than the definition, to calculate the integral?
The answer to these two questions is not easy: a characterization of integrable functions is given by a theorem from Vitali and Lebesgue, while a technique to calculate integrals of a wide class of functions comes as a consequence of the Fundamental theorem of calculus (Torricelli's theorem). There is no simple technique that allows us to calculate every integral and, in many cases, only numerical methods can be applied.
Trapezoids
If f is a non negative function in the interval
[a,b], we call a trapezoid the set 
, that is the set of all points of the cartesian
plane between the function and the x-axis.
If f is Riemann integrable, we define the area
of the trapezoid to be the integral 
.
If the function is non positive we may again call a
trapezoid the set of all points of the cartesian plane
between the x-axis and the function: in this case the
region is under the x-axis, and the integral will be the negative area of the trapezoid.
As with step functions, if a>b, we define 
(in this case the domain of the function is
[b,a]), and 
.
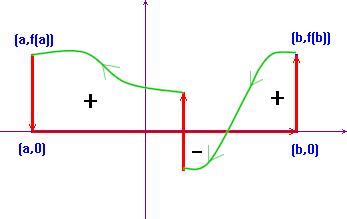
Now consider a path from (a,0), to (b,0), to
(b,f(b)), to (a,f(a)) (along the graph of the
function, when possible), and again to (a,0). This path
encloses some regions, whose contour is sometimes clockwise and
sometimes counterclockwise directed. We'll consider as
positive the areas whose contour is counterclockwise directed,
as negative those whose contour is clockwise directed. One can
prove that the is the algebraic sum of
all these areas.
