Other definitions of the Riemann integral
One can introduce the Riemann integral using other techniques: we'll mention here some of them. It can be proved that all definitions are equivalent, and choosing one or another is only a matter of convenience.
In the following f is a bounded function over an
interval [a,b], and 
is a dissection of [a,b].
Riemann-Cauchy sums
A
Riemann-Cauchy sum of f with respect
to the dissection D is defined as: 
,
where 
is an arbitrary point chosen in the
interval 
.
Let's call σ the maximum of the lengths of the intervals determined by the dissection D. We may consider what happens of Riemann-Cauchy sums when we consider dissections corresponding to very small values of σ. The problem is not simple because given a value of σ, there are many different Riemann-Cauchy sums: a Riemann-Cauchy sum is not a function of the only variable σ. So it is not possible to calculate a limit, in the usual sense, as σ tends to zero. Even so we'll give the following informal "definition":
A function is Riemann integrable if the limit of the Riemann-Cauchy sums, as σ tends to zero, exists and is a finite number I: this number is called the Riemann integral of the function.
This definition has an important geometric meaning, that is particularly simple to illustrate for non negative functions. Consider a dissection of [a,b] such that σ is "infinitely small": then there is basically one only point in each interval determined by the dissection, and the corresponding Riemann-Cauchy sum is almost exactly the Riemann integral of the function. This integral is the sum of the areas of a great number of rectangles with length xi-xi-1 and height f(ti), as the picture here below shows. This is one of the techniques used in numerical analysis to evaluate integrals.
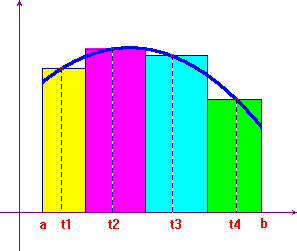
The symbol currently used for Riemann integrals originates from
this geometric interpretation. In 
you can interpret:
-
the symbol
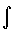as a modification of the
summation symbol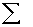 
;
- the f(x) as the value of the function in the one of the points of the interval [a,b] (remember that, as all the intervals determined by the dissection are infinitely small, their number is infinite and each of them contains basically one point);
- the dx as the length of the intervals determined by the dissection (that is approximately zero);
- the product f(x)dx as the area of an infinitely thin rectangle of length dx and height f(x);
- finally the integral itself as the sum of all these areas (infinite areas, each of which is infinitely small).
Upper and lower Riemann sums
Call Si and Ii the supremum and infimum of the function in each interval determined by the dissection. Then
-
the upper sum of f with respect to
the dissection D is defined as:
;
-
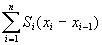the lower sum of f with respect to
the dissection D is defined as:
.
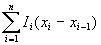The upper sums are always greater than the lower sums, and the infimum of upper sums and the supremum of lower sums are always finite.
A function is Riemann integrable if the infimum of upper sums and the supremum of lower sums coincide: the common value is the Riemann integral of the function.
This definition is almost the same as the one we have given using step functions: upper and lower sums are basically the integrals of upper and lower step approximations of the function f. The difference is that here we do not consider all the lower and upper approximations, but the theory one obtains with the two definitions is the same.
Uniform dissections
Till now we have considered general dissections of the interval [a,b]: this is useful in many circumstances. However it's sometimes better to use uniform dissections, that is dissections where the length of all intervals is the same: (b-a)/n.
It can be proved that even if one introduces this particular limitation in the choice of the possible dissections the resulting theory is completely equivalent, in the sense that the integrable functions and the values of the integrals remain the same. We'll sometimes use this possibility in what follows.