Problemi riepilogativi di analisi delle funzioni reali di variabile reale - 1
Problema 1
Si consideri l'ellisse di equazione ![]() e l'iperbole di equazione xy=k; si determini il valore
positivo di k in corrispondenza del quale le due curve risultano tangenti. Detti
A il
punto, di ascissa positiva, di intersezione dell'ellisse con l'asse x,
B il
punto di tangenza, appartenente al primo quadrante, tra le due curve, C il punto, del primo
quadrante, comune alla retta y=mx (con m>0) e all'iperbole sopra trovata, si
dica come deve essere scelto m affinché l'ordinata di C sia maggiore di
quella di B. Posto m=6 e detta H la proiezione di C sull'asse delle
x, si determini il volume del solido ottenuto da una rotazione completa, attorno
all'asse delle x, della figura limitata dai segmenti CH,
HA, dall'arco
AB di ellisse e dall'arco BC di iperbole.
e l'iperbole di equazione xy=k; si determini il valore
positivo di k in corrispondenza del quale le due curve risultano tangenti. Detti
A il
punto, di ascissa positiva, di intersezione dell'ellisse con l'asse x,
B il
punto di tangenza, appartenente al primo quadrante, tra le due curve, C il punto, del primo
quadrante, comune alla retta y=mx (con m>0) e all'iperbole sopra trovata, si
dica come deve essere scelto m affinché l'ordinata di C sia maggiore di
quella di B. Posto m=6 e detta H la proiezione di C sull'asse delle
x, si determini il volume del solido ottenuto da una rotazione completa, attorno
all'asse delle x, della figura limitata dai segmenti CH,
HA, dall'arco
AB di ellisse e dall'arco BC di iperbole.
Problema 2
Detti P(x) e Q(x) due polinomi, si consideri la funzione razionale fratta ![]() . Si determinino i due
polinomi in modo che:
. Si determinino i due
polinomi in modo che:
-
il polinomio in due variabili yQ(x)-P(x) sia di terzo grado;
-
la funzione abbia come unico asintoto verticale la retta x+1=0;
-
la funzione abbia come unico asintoto orizzontale la retta 7y+10=0;
-
la funzione abbia un estremo relativo nel punto A(-2,-38/7);
-
il coefficiente del termine di grado massimo del numeratore sia -10.
Tracciare il grafico della funzione così ottenuta.
Problema 3
Si consideri la funzione 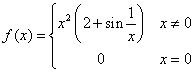 . Si dimostri che vale la seguente disuguaglianza per f(x):
. Si dimostri che vale la seguente disuguaglianza per f(x): ![]() . Se ne deduca che la funzione
ha, per x=0, un minimo relativo proprio che è anche minimo assoluto. Si dimostri poi che la
funzione è derivabile per ogni x, calcolando anche la derivata prima. Si dimostri
ancora, per sostituzione diretta, che la derivata prima è negativa nei punti di ascissa
. Se ne deduca che la funzione
ha, per x=0, un minimo relativo proprio che è anche minimo assoluto. Si dimostri poi che la
funzione è derivabile per ogni x, calcolando anche la derivata prima. Si dimostri
ancora, per sostituzione diretta, che la derivata prima è negativa nei punti di ascissa ![]() , mentre è
positiva nei punti di ascissa
, mentre è
positiva nei punti di ascissa ![]() , con k≠0. Se ne deduca che la funzione non è
decrescente
a sinistra e crescente a destra. Questo risultato è in contrasto con qualcuno dei
teoremi noti sui limiti?
, con k≠0. Se ne deduca che la funzione non è
decrescente
a sinistra e crescente a destra. Questo risultato è in contrasto con qualcuno dei
teoremi noti sui limiti?
Problema 4
In un piano riferito ad un sistema di assi cartesiani ortogonali xOy, si consideri la
circonferenza di centro l'origine e raggio 1. Sia A il punto di questa
circonferenza appartenente al primo quadrante e con ascissa ![]() . Si consideri un punto M sull'asse
delle ascisse in modo che la parallela all'asse delle ordinate condotta per M incontri la
circonferenza nei due punti P e Q. Scelta come incognita l'ascissa
x del
punto M si studi la funzione che rappresenta l'area del triangolo
APQ,
determinando in particolare per quale valore di x essa assume valore massimo e ricercando
eventuali punti di non derivabilità per la funzione.
. Si consideri un punto M sull'asse
delle ascisse in modo che la parallela all'asse delle ordinate condotta per M incontri la
circonferenza nei due punti P e Q. Scelta come incognita l'ascissa
x del
punto M si studi la funzione che rappresenta l'area del triangolo
APQ,
determinando in particolare per quale valore di x essa assume valore massimo e ricercando
eventuali punti di non derivabilità per la funzione.
Si studi poi la funzione ![]() e si calcoli l'area della regione finita di piano compresa tra le due curve, la
retta
e si calcoli l'area della regione finita di piano compresa tra le due curve, la
retta ![]() e la retta
x=1.
e la retta
x=1.
Si consideri di nuovo la funzione rappresentante l'area del triangolo. Posto
x=t e
y=s, si interpreti la s come l'ascissa raggiunta da un punto su una retta al
variare del tempo t e si descriva il moto del punto, spiegando in particolare che cosa
succede nell'istante ![]() .
.
Problema 5
Si consideri la funzione ![]() .
.
-
Trovarne l'insieme di definizione.
-
Dire in quali punti è continua.
-
Calcolare i limiti notevoli e gli eventuali asintoti.
-
E' possibile prolungarla per continuità in x=0?
-
Calcolare la derivata prima per x≠1.
-
Perché il calcolo precedente non ha senso per x=1?
-
Calcolare i limiti delle derivata prima per x tendente a zero da destra e ad 1 da destra e da sinistra e dedurne le conseguenze.
-
Determinare i massimi e minimi relativi ed assoluti.
-
Tracciare un grafico indicativo dei risultati fin qui raggiunti.
-
Trovare, per x≠1, la derivata seconda della funzione e determinare i flessi.
-
Perché non si può calcolare la derivata seconda nel punto 1?
Problema 6
Determinare il numero ed il segno delle soluzioni della equazione: ![]() .
.
Problema 7
Si consideri una semicirconferenza di centro O e diametro AB=2r, e sopra di essa si prendano due punti C e D, con C più vicino ad A. Sia E il punto di intersezione delle rette AC e BD.
-
Dimostrare che i due triangoli ABE e CDE sono simili.
-
Supposto CD=(14/25)r, e posto
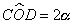 si determinino il seno ed il coseno dell'angolo
α.
si determinino il seno ed il coseno dell'angolo
α. -
Si indichi con H la proiezione di O su CD. Dimostrare che l'angolo HCO è uguale all'angolo BEA e determinarne il seno e coseno.
-
Dopo aver posto BEA=x, studiare, nei limiti posti dal problema, la funzione
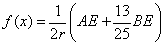 .
.
Problema 8
Si consideri la disequazione x2 ≤ h+x3 (con x>0 e h costante non negativa). Si determini il più piccolo valore di h per cui essa risulta identicamente verificata.
Problema 9
Data la famiglia di funzioni f(x)=(m-2)x3-mx+2, dove m è un parametro reale, si dimostri che, al variare di m tutte passano per tre punti A, B, C, di cui si chiedono le coordinate. Si provi anche che i tre punti sono allineati. Si determini, al variare di m, la crescenza e decrescenza delle funzioni e si dica in particolare per quali valori di m esse ammettono massimi e minimi. Si studi la curva corrispondente al valore m=4.
Problema 10
Si determini l'equazione della parabola del tipo y=ax2+bx+c, passante per
i punti A(-1,7), B(2,4), C(½,1). Fra le curve del tipo ![]() , si determini quella tangente alla parabola e la
si rappresenti graficamente.
, si determini quella tangente alla parabola e la
si rappresenti graficamente.
Problema 11
Con riferimento ad un sistema di assi cartesiani ortogonali xOy:
-
Si tracci il grafico della funzione
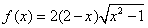 .
. -
La retta x=2 interseca l'iperbole equilatera di equazione x2-y2=1 nei punti A e B. Si inscriva nel segmento iperbolico di base AB il rettangolo di area massima. A tal fine si indichi con t l'ascissa di due vertici del generico rettangolo inscritto nel segmento iperbolico e si utilizzi la curva sopra studiata.
-
Si determini il volume del solido generato in una completa rotazione attorno all'asse x dalla superficie piana finita delimitata dalla curva studiata al punto 1 e dall'asse x.
Problema 12
Si dimostri che ogni cubica razionale intera (y=ax3+bx2+cx+d) ha un centro di simmetria. Si verifichi che tale centro è l'unico punto di flesso della curva. Si spieghi perché una tal funzione ha sempre un unico punto di flesso.
Problema 13
Si consideri la funzione ![]() . Si trovi, per via elementare, se essa è crescente o decrescente. La
crescenza o decrescenza può anche essere determinata mediante lo studio della derivata?.
. Si trovi, per via elementare, se essa è crescente o decrescente. La
crescenza o decrescenza può anche essere determinata mediante lo studio della derivata?.
Problema 14
Si studi la funzione ![]() . Si dica perché non c'è contrasto tra i risultati dello studio di
questa funzione e il corollario del teorema di Lagrange che riguarda le funzioni a derivata
nulla.
. Si dica perché non c'è contrasto tra i risultati dello studio di
questa funzione e il corollario del teorema di Lagrange che riguarda le funzioni a derivata
nulla.
Problema 15
Sia data la parabola ![]() ed un punto A(0,b), con b>0 numero reale fissato. Si trovi la
minima distanza tra A ed un generico punto della parabola.
ed un punto A(0,b), con b>0 numero reale fissato. Si trovi la
minima distanza tra A ed un generico punto della parabola.
Problema 16
Si consideri la funzione ![]() , ove m è un numero reale.
, ove m è un numero reale.
-
Determinare per quali valori di m tale funzione ammette massimi o minimi relativi.
-
Determinare per quali valori di m tale funzione è sempre crescente o sempre decrescente.
-
Mostrare che al variare di m tutte le curve grafico della funzione data passano per uno stesso punto di cui si chiedono le coordinate.
-
Determinare m in modo che la tangente in P alla curva sia parallela alla retta di equazione 14x+9y+18=0. Studiare la funzione corrispondente a questo valore di m.
Problema 17
Si disegni il grafico della funzione ![]() , determinando: l'insieme di definizione, i limiti notevoli, gli
asintoti, i massimi e minimi relativi, la concavità e convessità. Si dica se la
funzione ha massimo e minimo assoluto e se esiste qualche punto in cui la funzione è
continua ma non derivabile.
, determinando: l'insieme di definizione, i limiti notevoli, gli
asintoti, i massimi e minimi relativi, la concavità e convessità. Si dica se la
funzione ha massimo e minimo assoluto e se esiste qualche punto in cui la funzione è
continua ma non derivabile.
Problema 18
Si consideri il triangolo ABC con AB= a. Posto AĈB=x e sapendo che AC=2BC, calcolare AC, BC e l'altezza CH relativa al lato AB in funzione di x. Studiare la funzione f(x)=CH/(2AB) nell'intervallo 0 ≤ x ≤ π.
Problema 19
Si consideri una circonferenza di raggio r e sia A un suo punto. Condurre per A la
tangente alla circonferenza e una corda AB in modo che un angolo tra la corda e la tangente sia di
π/3. Sul più piccolo dei due archi AB di circonferenza si prenda un punto M. Sia N il
punto di intersezione tra la retta BM e la tangente in A alla circonferenza. Detto
x
l'angolo ABM si studi, nei limiti posti dal problema, la funzione ![]() . Calcolare l'area
della regione finita di piano compresa tra il grafico della predetta funzione e l'asse delle
x.
. Calcolare l'area
della regione finita di piano compresa tra il grafico della predetta funzione e l'asse delle
x.
Problema 20
Si consideri la funzione ![]() . Tracciarne il grafico determinando anche i punti di flesso e studiando la
concavità. Trovare poi l'equazione delle parabole passanti per il punto di flesso della
f, aventi in questo punto la medesima tangente di f e tali che l'area della
regione finita di piano compresa tra le parabole, la curva grafico della funzione, la retta
x=0 e la retta x=1/2, sia uguale a 1.
. Tracciarne il grafico determinando anche i punti di flesso e studiando la
concavità. Trovare poi l'equazione delle parabole passanti per il punto di flesso della
f, aventi in questo punto la medesima tangente di f e tali che l'area della
regione finita di piano compresa tra le parabole, la curva grafico della funzione, la retta
x=0 e la retta x=1/2, sia uguale a 1.
Problema 21
Si consideri la funzione ![]() . Tracciarne il grafico determinando anche i punti di flesso e studiando la
concavità. Trovare una traslazione di assi in modo che la funzione assuma la forma
. Tracciarne il grafico determinando anche i punti di flesso e studiando la
concavità. Trovare una traslazione di assi in modo che la funzione assuma la forma ![]() , con opportuni valori
di a, b, c. Che cosa se ne deduce sulle simmetrie della funzione data?
, con opportuni valori
di a, b, c. Che cosa se ne deduce sulle simmetrie della funzione data?
Considerata, nel nuovo sistema di assi, la funzione g, si determini una retta passante per l'origine, che intersechi la curva in due punti M ed N, in modo che il segmento MN risulti minimo. Verificare che la retta, r, così trovata è una delle bisettrici degli angoli formati dagli asintoti della curva.
Si consideri una retta perpendicolare alla retta r, in modo che incontri la curva in due punti P e Q. Verificare che il luogo geometrico descritto dal punto medio del segmento PQ coincide con la retta r, privata del segmento MN. Che cosa se ne può dedurre sulle simmetrie della funzione data?
Problema 22
Si consideri la funzione ![]() . Trovare una traslazione di assi in modo tale che la funzione assuma la forma
Y=k/X, con un opportuno valore di k.
. Trovare una traslazione di assi in modo tale che la funzione assuma la forma
Y=k/X, con un opportuno valore di k.
Generalizzare la questione, trovando sotto quali condizioni per i coefficienti
a, b, c, d
la funzione ![]() può essere scritta nella forma Y=k/X. Provare che, viceversa, data una qualunque
funzione della forma y=k/x, con un'opportuna traslazione di assi essa si muta in una
funzione della forma
può essere scritta nella forma Y=k/X. Provare che, viceversa, data una qualunque
funzione della forma y=k/x, con un'opportuna traslazione di assi essa si muta in una
funzione della forma ![]() , con opportuni valori dei coefficienti.
, con opportuni valori dei coefficienti.
Problema 23
Si consideri la funzione ![]() .
.
-
Si determinino le costanti reali a, b, c, d, h in modo che la funzione abbia la retta x=1 come asintoto verticale, che abbia un massimo relativo nel punto (0,0) e che nel punto di ascissa 2 abbia per tangente la retta y = 4x - 8.
-
Si studi la funzione ottenuta al punto a).
-
Sia t un reale strettamente maggiore di 1 e diverso da 2. Si calcoli l'area della regione finita di piano compresa tra l'asintoto obliquo, la curva, la retta x=2 e la retta x=t, distinguendo i casi t<2 e t>2. Detta s(t) quest'area, si calcoli, se t>2 il
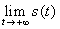 , se t<2, il
, se t<2, il 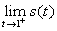 .
. -
Tra tutte le parabole passanti per i punti che la curva ha in comune con l'asse delle ascisse, si determinino quelle tali che l'area della regione finita di piano compresa tra la retta x=-1, l'asse delle y e le due curve sia uguale a 7/3-ln2.
-
Delle parabole trovate al punto d) si consideri quella che ha derivata seconda positiva e si determinino tutte le sue intersezioni con la funzione già studiata. Si indichino con O ed A i due punti di ordinata nulla (A è quello di ascissa positiva), con E il punto di ordinata negativa, con F quello di ordinata positiva. Si calcoli l'area delle regioni di piano limitate dalla parabola e dalla funzione. Si determini l'equazione della circonferenza passante per O ed A e avente centro sulla retta EF. Si calcoli l'area delle regioni finite di piano limitate dalla circonferenza e dalla parabola. Considerata la regione di piano di area minore si determini il volume del solido ottenuto da una sua completa rotazione attorno all'asse delle x.
-
Si consideri la funzione
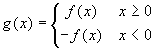 . Si dica se essa è continua e derivabile per x=0. Utilizzando i
risultati ottenuti per se ne disegni il grafico.
. Si dica se essa è continua e derivabile per x=0. Utilizzando i
risultati ottenuti per se ne disegni il grafico. -
Utilizzando i risultati già ottenuti per la funzione f si studi la funzione
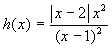 , determinando in
particolare eventuali punti in cui non è derivabile.
, determinando in
particolare eventuali punti in cui non è derivabile. -
Utilizzando i risultati già ottenuti per la funzione f si studi la funzione
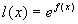 , limitando
l'indagine alla derivata prima.
, limitando
l'indagine alla derivata prima. -
Si considerino nuovamente la parabola e la circonferenza determinate al punto e). Nel semipiano delle y positive si conduca una retta parallela all'asse x che intersechi la circonferenza nei due punti M ed N. Condotte da M ed N le parallele all'asse y fino ad incontrare la parabola nei punti R ed S rispettivamente, si determini la posizione della suddetta retta in modo che il rettangolo MNSR abbia area massima.
-
Si consideri la retta y=mx. Si dica per quali valori di m essa interseca la curva in due punti U e V diversi dall'origine e si determini il luogo geometrico descritto dal punto medio del segmento UV al variare di m.
-
Si consideri la retta y=m(x-2). Determinare per quali valori di m la retta incontra la curva in due punti T e Z diversi da (2,0) e si determini il luogo geometrico descritto dal punto medio del segmento TZ, tracciandone anche il grafico.
Problema 24
Si consideri una circonferenza di centro O e raggio r=1. Sia AB un suo diametro. Sul
prolungamento di AB, dalla parte di B, si prenda un punto C in modo che BC=1 e si conduca la
tangente alla circonferenza per B. Per C si conduca una secante alla circonferenza che intersechi
la tangente in B nel punto P e la circonferenza nei due punti M ed N (con PM>PN). Detto H il
piede della perpendicolare condotta da O alla retta CM, si ponga OH=x e si determinino i
limiti per x. Si consideri poi la funzione ![]() . Studiarla in tutto il suo dominio, limitando
l'indagine alla derivata prima.
. Studiarla in tutto il suo dominio, limitando
l'indagine alla derivata prima.
Problema 25
Si consideri la semicirconferenza di diametro AB=2r e si tracci la corda ![]() . Sull'arco AC si consideri
un punto M e si ponga MÂC=x. Si consideri la funzione f(x) = MC/AM. Si
studi questa funzione tracciandone un grafico indicativo.
. Sull'arco AC si consideri
un punto M e si ponga MÂC=x. Si consideri la funzione f(x) = MC/AM. Si
studi questa funzione tracciandone un grafico indicativo.