L'attrito statico
Consideriamo un corpo P appoggiato sopra una superficie S (che supporremo piana per semplicità), e indichiamo con N la forza normale che preme P su S. In molti casi di interesse pratico questa forza è la componente del peso perpendicolare alla superficie di appoggio, ma possono anche presentarsi situazioni diverse, come un agente esterno che preme sul corpo. In una vasta classe di situazioni, di grande interesse pratico, le interazioni tra il corpo appoggiato e la superficie di appoggio, molto complesse se esaminate da un punto di vista microscopico, possono essere schematizzate in maniera abbastanza semplice, seppure solo in prima approssimazione. Se, come supporremo, il corpo non può penetrare nella superficie, questa interazione ha una prima componente esattamente opposta ad N (la chiameremo reazione normale) e una seconda componente tangente ad S (con verso tale da "ostacolare il moto") ed è questa componente che chiameremo attrito.
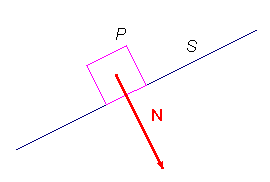
Le leggi dell'attrito forniscono un legame tra la componente tangente della interazione tra P ed S (che abbiamo, appunto, chiamato attrito) e l'ambiente circostante, cioè le caratteristiche di P ed S, ed in particolare delle superfici di contatto.
Si verifica sperimentalmente che la situazione risulta essere diversa nel caso di moto relativo tra P ed S rispetto al caso di quiete tra P ed S. Il primo caso costituisce il cosiddetto attrito dinamico, il secondo il cosiddetto attrito statico. Ci occuperemo per prima dell'attrito statico.
La legge dell'attrito statico esprime la massima forza di attrito esercitabile tra due superfici asciutte non lubrificate e soddisfa le seguente leggi empiriche:
- E' approssimativamente indipendente, entro grandi limiti, dall'area della superficie di contatto.
- E' proporzionale alla forza normale premente, secondo una costante, detta coefficiente di attrito statico, che dipende dal tipo di superfici e dal loro grado di levigatura. La costante può anche essere maggiore di uno, sebbene sia comunemente minore di uno.
Queste leggi empiriche possono essere compendiate nella formula:
,
dove As rappresenta l'attrito statico e ks il coefficiente di attrito statico.
E'
molto importante il fatto che la legge dell'attrito statico
non è un'equazione, cioè non fornisce
direttamente il modulo della forza di attrito effettivamente
esercitata: è invece una disequazione, da cui si
può unicamente ricavare il modulo della massima forza
esercitabile nelle condizioni date. Per determinare il valore
effettivo della forza di attrito occorrerà utilizzare
l'equazione della dinamica (con accelerazione nulla!).
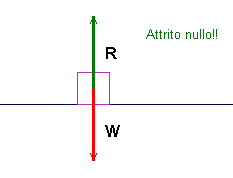
Si noti che l'attrito si manifesta solo se
sollecitato, cioè solo se esistono forze che
tendono a far muovere una superficie rispetto all'altra. Si
consideri, per esempio, il corpo P appoggiato su un
piano orizzontale S, nell'ipotesi che l'unica
forza esterna agente sia il peso, W, di
P. Allora il piano di appoggio reagirà con una
forza, R, perpendicolare al piano stesso,
esattamente come se non ci fosse alcun attrito. Si osservi che
la legge dell'attrito statico è verificata, in quanto
.
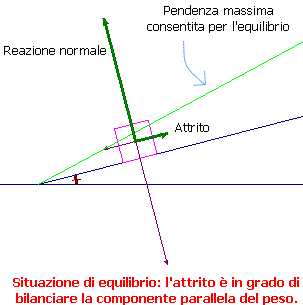
Esaminiamo ora una situazione comune nelle applicazioni: il
corpo P è appoggiato su un piano S,
inclinato di un angolo θ, rispetto all'orizzontale e
sottoposto solo all'azione della forza peso. Il corpo
è sollecitato a muoversi dalla componente del peso
parallela al piano inclinato: 
. Dunque l'attrito è sollecitato e,
se consentito dalla legge dell'attrito statico,
impedirà il moto del corpo. In caso contrario il corpo si
muoverà verso il basso e le considerazioni relative al
caso statico non saranno più valide. In sostanza se il
corpo rimane fermo significa che l'attrito è in grado
di bilanciare esattamente la componente parallela del peso, per
cui l'attrito stesso avrà modulo 
; se invece il corpo si mette in moto significa che la
componente parallela del peso è, in modulo, più
grande del massimo attrito possibile, e allora non
riuscirà ad impedire il moto.
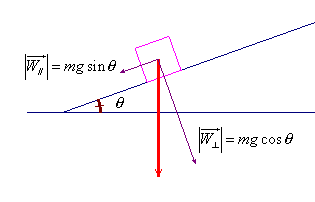
E' chiaro che più grande è l'inclinazione
del piano, minore sarà il massimo attrito possibile,
perché all'aumentare dell'inclinazione diminuisce
la componente perpendicolare del peso (in quanto contiene il
coseno dell'angolo) e il massimo attrito possibile è
proporzionale a questa componente; per contro all'aumentare
dell'inclinazione del piano aumenta la componente parallela
del peso (in quanto contiene il seno dell'angolo). E'
allora evidente che il massimo angolo, diciamolo σ, che
consente l'equilibrio è quello per cui 
, ovvero tgσ = ks.
Questa osservazione consente una semplice determinazione
sperimentale di ks: basta appoggiare un
corpo su un piano e inclinare il piano fin tanto che il corpo
comincia a muoversi; la tangente dell'angolo per cui inizia
il movimento è il coefficiente di attrito statico
cercato.
Si osservi anche che, siccome all'aumentare dell'inclinazione aumenta la componente parallela del peso, aumenta anche l'attrito effettivamente esercitato (che è, appunto, opposto a questa componente del peso), fin quando si raggiunge il massimo angolo, σ, che consente l'equilibrio: a questo punto occorre considerare la situazione di attrito dinamico. Si vedano le due figure qui sotto.
