I postulati della relatività ristretta e le trasformazioni di Lorentz
La relatività ristretta si basa sui seguenti due postulati, di cui il primo (Postulato di relatività ) costituisce una generalizzazione a tutti i fenomeni del Principio galileiano di relatività, il secondo assume direttamente il risultato dell'esperimento di M.M.
-
Le leggi della fisica sono le stesse in tutti i riferimenti inerziali.
-
La velocità della luce è una costante universale, indipendente non solo dal moto della sorgente, ma anche da quello dell'osservatore (naturalmente nel caso di moti rettilinei ed uniformi).
E' da segnalare che, storicamente, l'influenza dell'esperimento di Michelson e Morley nella formulazione della teoria della relatività fu, tutto sommato, piuttosto marginale e che invece grande importanza ebbe lo studio dei problemi connessi con la forza di Lorentz su una carica in moto.
Il primo dei postulati sopra riportati costituisce una estensione, e non una negazione, del principio di relatività galileiana; il secondo sostituisce il tempo assoluto della fisica classica con una velocità assoluta, quella della luce.
Come prima conseguenza di questi due postulati vogliamo ricavare, anche se con una trattazione qualitativa, le formule che legano le coordinate di due eventi visti da due diversi sistemi di riferimento in moto rettilineo ed uniforme uno rispetto all'altro.
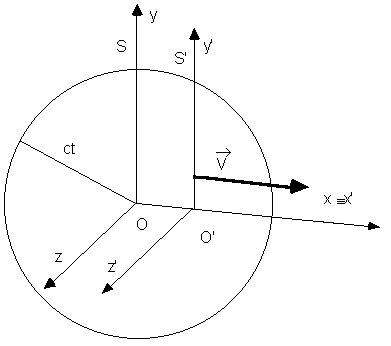
Si consideri, vedi figura qui sopra, una sorgente luminosa, posta nell'origine di un sistema di riferimento S. All'istante iniziale i due riferimenti coincidano. S ed S' siano muniti di due orologi, preventivamente sincronizzati, per esempio ponendo t'=0 quando t=0. In questo istante la sorgente posta in O emette un'onda luminosa. Dopo un certo tempo t il fronte d'onda, visto da S, sarà una superficie sferica di centro O e raggio ct, essendo c la velocità dell'onda. Questa superficie avrà dunque equazione x2+y2+z2=c2t2. Per il principio di relatività questo fronte d'onda deve essere visto come una sfera anche da S', il quale, altrimenti, potrebbe accorgersi dalla diversa forma del fronte d'onda di essere in movimento rispetto ad S. (In questo discorso é fondamentale l'assenza del mezzo di propagazione: un ragionamento analogo non vale per le onde acustiche e in generale per le onde meccaniche). Naturalmente le coordinate saranno ora x',y',z' e il tempo sarà, probabilmente, diverso: t'. La velocità deve però essere la stessa (2° postulato di relatività). Il fronte d'onda visto da S' deve dunque avere equazione x'2+y'2+z'2=c2t' 2.
Se sostituiamo in quest'ultima equazione le trasformazioni
di Galileo otteniamo
x2-2xVt+V2t2+y2+z
2=c2t2, che non é in
accordo con l'equazione vista da S. Cerchiamo una
trasformazione che elimini i termini indesiderati. Poiché
i termini in y e z vanno bene dobbiamo modificare quelli in x e
in t. Proviamo con una trasformazione del tipo x'=x-Vt,
y'=y, z'=z, t'=t+αx, con α da
determinare. (Questa scelta é dettata dal fatto che la
trasformazione che cerchiamo non deve essere "troppo
diversa" da quella di Galileo, e inoltre deve essere
"semplice"). Sostituendo troviamo
x2-2xVt+V2t2+y2+z
2=c2t2+2c2αtx+c
2α2x2. I termini in xt si
eliminano se prendiamo 
. Posto 
, resta
x2(1-β2)+y2+z2=c
2t2(1-β2), che presenta ancora
qualche coefficiente indesiderato. Posto ora 
, se prendiamo:
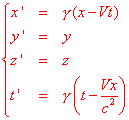
tutto funziona, nel senso che un'equazione si riduce, per cambiamento di coordinate, esattamente all'altra. La trasformazione considerata é l'unica che risolve tutti i nostri problemi. Essa sostituisce la trasformazione galileiana ed é nota come trasformazione di Lorentz, in quanto Lorentz la trovò per primo, con la sola richiesta che essa rendesse invarianti le equazioni di Maxwell. Si noti come, in questa trasformazione di Lorentz, la prima e l'ultima riga siano, a parte la presenza di c2, perfettamente simmetriche.
La solita differenziazione permette di scrivere le formule per la composizione delle velocità:
.
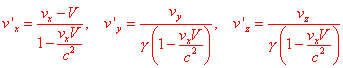É interessante vedere come operano queste formule su alcuni semplici esempi. Quello che ci interessa è comunque il fatto che la loro conseguenza fondamentale è che componendo velocità minori di quella della luce si ottengono ancora velocità minori di quella della luce.