Punti notevoli di un triangolo
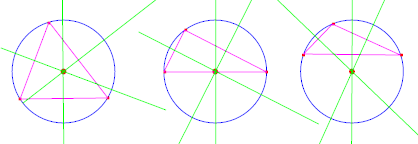Circocentro: è il punto di
intersezione degli assi dei lati di un triangolo. É il
centro della circonferenza circoscritta al triangolo. Nei
triangoli acutangoli è interno al triangolo, nei
triangoli rettangoli coincide con il punto medio
dell'ipotenusa, nei triangoli ottusangoli è esterno
al triangolo.
"O cara piota mia che sì t'insusi,
che, come veggion le terrene menti
non capere in triangol due ottusi,
D.C. 3, XVII, 13-15
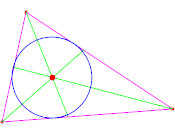Incentro: è il punto di incontro
delle bisettrici degli angoli interni di un triangolo. É
il centro della circonferenza inscritta nel triangolo ed
è sempre interno al triangolo.
Ortocentro: è il punto di
intersezione delle altezze di un triangolo, o dei loro
prolungamenti. É interno al triangolo per i triangoli
acutangoli, coincide con il vertice dell'angolo retto per i
triangoli rettangoli, è esterno al triangolo per i
triangoli ottusangoli. É anche il centro
radicale dei tre cerchi che hanno come diametro i lati del
triangolo.
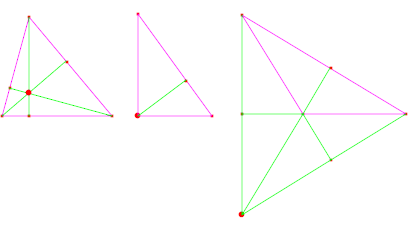
Baricentro: è il punto di
incontro delle mediane di un triangolo. É sempre interno
al triangolo e gode della seguente proprietà:
ciascuna mediana è divisa dal baricentro in due
parti, di cui quella contenente il vertice è doppia
dell'altra. Se, in un piano cartesiano, sono note le
coordinate dei vertici, il baricentro ha come coordinate le
medie aritmetiche delle coordinate degli estremi: 
. Nel caso di un triangolo omogeneo, o di tre punti di
uguale massa disposti nei vertici, il baricentro coincide con il
centro di gravità o di massa (usualmente spesso chiamato
ancora baricentro).
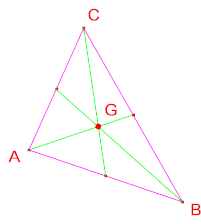
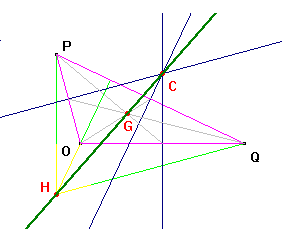Retta di Eulero: in ogni triangolo
l'ortocentro, il baricentro e il circocentro sono allineati; la
retta cui appartengono si chiama retta di Eulero; inoltre HG=2GC.
Puoi anche vedere un'animazione di questa
figura.