Potenza di un punto rispetto ad un circolo. Asse radicale di due circoli.
Data una circonferenza centro O e raggio r e un punto Q ad essa esterno, si considerano una secante e una tangente condotte da Q; per il teorema della secante e della tangente il prodotto QA·QB è sempre uguale a QT2, ed è quindi indipendente dalla particolare secante considerata. Questo prodotto si chiama potenza p del punto Q rispetto al circolo, cioè si pone:
p = QA·QB.
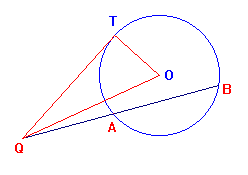
Dal teorema di Pitagora applicato al triangolo QOT si ottiene p = QO2-r2. Se consideriamo un sistema di coordinate cartesiane ortogonali, l'equazione della circonferenza è f(x,y)=0, dove f(x,y)=x2+y2+ax+by+c=(x-xC) 2+(y-yC)2-r2, con evidente significato dei simboli..
Se Q ha coordinate (s,t), si ha anche QO2=(s-xC)2+(t-yC) 2. Se ne deduce subito che p=(s-xC)2+(t-yC)2-r 2=f(s,t), cioè la potenza di Q si ottiene semplicemente sostituendo le sue cooordinate nell'equazione cartesiana della circonferenza.
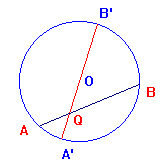
Se il punto Q è interno alla circonferenza, invocando il teorema delle due corde si deduce ancora che il prodotto QA·QB dei segmenti della figura qui sotto è indipendente dalla particolare corda condotta per Q. Si ha inoltre QA·QB=QA'·QB'=(r-QO)·(r+QO)=r 2-QO2. Per mantenere la situazione di prima si pone ora p = -QA·QB. E' immediato che si ha, come prima, p=f(s,t).
Se infine Q è sul circolo la potenza è, per definizione, zero. In ogni caso vale dunque la formula p=f(s,t).
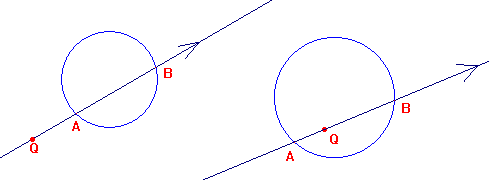
Per uniformare i due casi di punto interno ed esterno alla circonferenza basta pensare alla retta passante per Q come orientata, e a QA e QB come misure con segno dei segmenti orientati rispettivi. Si esaminino le due situazioni qui sotto: nella prima QA e QB sono concordi, nella seconda discordi, qualunque sia l'orientamento della retta.
Dunque si può definire potenza di un punto Q del piano rispetto ad un circolo dello stesso piano il prodotto
![]()
delle misure orientate dei segmenti QA e
QB individuati sul circolo dato da un retta
orientata qualunque che lo intersechi. Quando ci sarà
bisogno utilizzeremo, per la potenza, il simbolo più
completo: ![]() (ovvero potenza di Q rispetto al
circolo di centro O).
(ovvero potenza di Q rispetto al
circolo di centro O).
Consideriamo ora due circoli non concentrici: ogni punto Q del piano ha una potenza rispetto ai due circoli e si può considerare il luogo dei punti che hanno la stessa potenza che è, come si può provare, una retta detta asse radicale dei due circoli. Questa retta è perpendicolare alla congiungente i centri e, se i due circoli hanno due punti in comune, è la retta che passa per questi due punti. Nel caso di due circoli concentrici l'asse radicale non è definita, in quanto non esistono punti del piano che hanno ugual potenza rispetto ai due cerchi: poiché all'avvicinarsi dei centri di due cerchi l'asse radicale si allontana all'infinito, si usa dire che, per due circoli concentrici, l'asse radicale è mandata all'infinito ( in geometria proiettiva si dice che è la retta impropria).
Dati tre circoli a due a due non concentrici si possono considerare tre assi radicali che, come si può provare, si intersecano in un punto detto centro radicale dei tre circoli, non appena i centri dei tre circoli non sono allineati.
A questo punto è facile costruire l'asse radicale di due circoli qualunque (ha interesse solo il caso che i circoli non si intersechino nè siano tangenti): basterà considerare un terzo circolo secante i due circoli dati, costruire i due assi radicali e il loro punto di interszione (centro radicale), e ricordare che quello richiesto deve essere perpendicolare alla congiungente i centri. Si veda la figura qui sotto Si può anche vedere un'animazione con CabriJava.
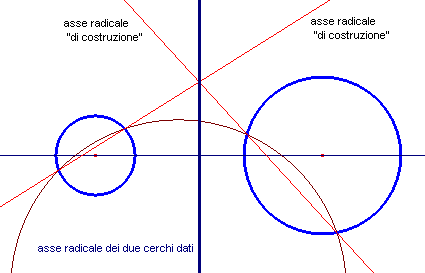
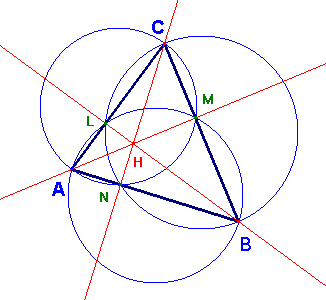
É interessante osservare che l'ortocentro di un triangolo è il centro radicale delle tre circonferenze che hanno come diametro i lati. Basta ricordare (si veda la figura qui sotto) che i triangoli BLA, BLC, AMB, AMC, CNA, CNB, sono rettangoli e quindi iscrivibili in una semicirconferenza. Puoi vedere un'animazione con Cabri.