Simultanéité, longueurs, temps
Considérons le schéma suivant.
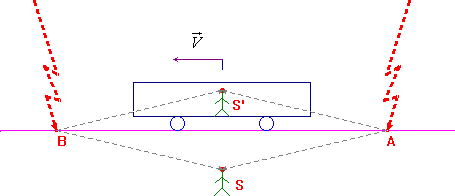
- A et B sont deux points sur une voie ferrée.
- Un train roule de A vers B.
- Un observateur S' se trouve dans le train.
- Un autre observateur S se tien au bord de la voie ferrée exactement a mi-chemin entre A et B.
- Deux éclairs vont toucher simultanément A et B, au moment précis où les deux observateurs sont opposés.
- Les deux observateurs disposent chacun d'un système de miroirs qui leur permettent de voir A et B sans bouger les yeux.
Que va-t-il se passer quand les deux éclairs vont tomber su r A et B? Pas de problèmes pour l'observateur S, il va les voir simultanément toucher A et B. L'observateur S', par contre, verra d'abord l'éclair B et ensuite l'éclair A. On doit changer l'idée de simultanéité et, par conséquence, l'idée même de temps!
Mais ce n'est pas encore fini: si nous voulont mesurer la longueur d'un objet nous devons marquer, au même instant, la position des deux bouts. Si l'objet ne bouge pas, il n'y a pas de problèmes, mais si l'objet a une vitesse, que veut dire "même instant"?
Même si ce n'est pas facile à prouver, nous sommes donc obligés de penser que:
- Si on mesure le temps, T, de vol d'un objet avec une montre qui est solidaire avec l'objet on obtient un temps plus petit que le temps, T', mesuré par une montre qui reste en terre. La montre en mouvement a ralenti. C'est la dilatation du temps: T' = γT.
- Si on mesure une longueur en mouvement avec un mètre solidaire à la longueur on obtient un résultat, L, plus grand que le résultat qu'on peut obtenir si la mesure, L', est faite avec un mètre solidaire à notre laboratoire. C'est la contraction des longueurs: L = γT'.