La transformation de Lorentz
Nous allons à présent examiner plus en détail les formules de Galilée et la loi de composition des vitesses. Nous pouvont retrouver dans ces formules les propriétés suivantes.
- Le mouvement n'est pas absolu: si on change le repère, la vitesse, et par conséquence la façon dont un corps bouge, change.
- Le temps est absolu: si on a synchronisé nos montres elles indiqueront toujours le même temps. Si je voyage entre Paris et New York avec mon super avion, sur ma montre je peut lire le temps de voyage, 2 heures et 5 minutes; ma femme, qui est à Paris, et mon fils, qui m'attend à New York, mesurent le même temps pour le trajet.
Malheureusement les choses ne sont pas si simples!
Avant tout le monde, Lorentz a supposé que les formules de Galilée ne sont pas exactes et qu'il est préférable de considérer les suivantes, désormais connues comme formules de la Transformation de Lorentz:
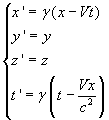 , ou
, ou
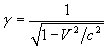 , et
c est la vitesse de la lumière.
, et
c est la vitesse de la lumière.
Personne n'aurait pu découvrir avant ces formules: la valeur de γ est tellement proche de un et la valeur de V/c2 est tellement proche de zéro qu'il est presque impossible d'apercevoir des différences entre la Transformation de Lorentz et les formules de Galilée, si V correspond à moins de 110.000.000 kilomètres par heure! N'oublions pas que la plus grande vitesse qu'un objet macroscopique ait atteint est de 100.000 kilomètres à l'heure, environ.
La conséquence plus importante de la Transformation de Lorentz est que le temps n'est plus absolu: ma montre sur le Concorde ne peut pas marquer le même temps que la montre de ma femme qui est restée à Paris!
La deuxième conséquence est la nouvelle formule pour l'addition des vitesses. Nous ecrivons simplement la formule concernant l'addition de deux vitesses parallèles à l'axe des abscisses:
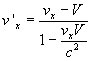 .
.
Si, par exemple, nous considèrons une particule qui voyage avec une vitesse c (vx = c), un observateur qui voyage à la vitesse V trouve la même vitesse, c, pour la particule! La vitesse de la lumière ne change pas si on change de repère.
Encore un exemple: Schumaker (S) avec sa Ferrari et Alonso (A) avec sa Renault voyagent, l'un vers gauche l'autre vers droite, à une vitesse de 0.9c (270.000 km/s). Quelle est la vitesse de Schumaker par rapport à Alonso? On considère la figure ci dessus
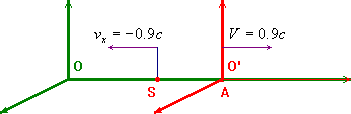
En appliquant la formule pour l'addition des vitesses nous trouvons: v'x = -0.994c, c'est-à-dire toujours une vitesse au-dessous de la vitesse de la lumière.