Le circonferenze tangenti a tre circonferenze date
Si tratta del problema di Apollonio vero e proprio e ci sono numerose possibili soluzioni con riga e compasso: ne proporremo due.
Prima costruzione
La prima delle soluzioni presentate è una delle più semplici: si tratta di applicare la stessa tecnica della dilatazione parallela già vista nel caso in cui erano date una retta e due cerchi. Si riduce la circonferenza di raggio più piccolo ad un punto e ci si riduce al caso di un punto e due circonferenze o di due punti e una circonferenza o di tre punti, a seconda del numero di circonferenze con raggio uguale presenti. Considerata la complessità della figura riportiamo solo la costruzione di due delle otto circonferenze cercate, nel caso in cui le tre circonferenze abbiano raggio diverso.
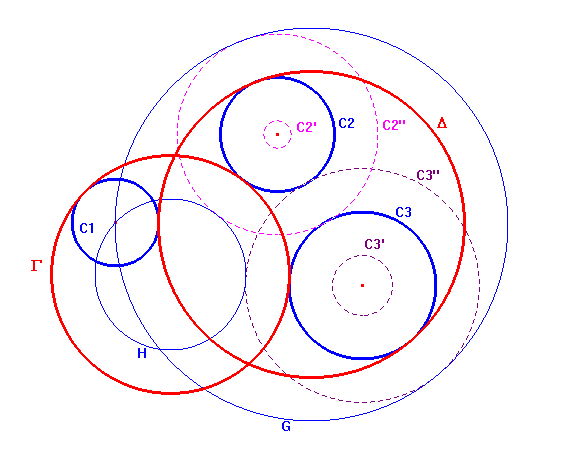
Le circonferenze date sono C1, C2, C3. La circonferenza C1 è stata ridotta al suo centro. Le circonferenze C2 e C3 sono state trasformate per dilatazione parallela in C2', C2", C3', C3". Le due circonferenze G ed H sono due delle quattro circonferenze passanti per il centro di C1 e tangenti a C2" e C3". Le circonferenze Γ e Δ sono due delle otto circonferenze cercate. Naturalmente per rendere leggibile la figura non abbiamo riportato tutte le linee di costruzione intermedie, in particolare quelle necessarie a costruire le circonferenze G ed H.
Seconda costruzione
La seconda costruzione presentata utilizza, oltre all'inversione, i fasci di circoli a punti limite.
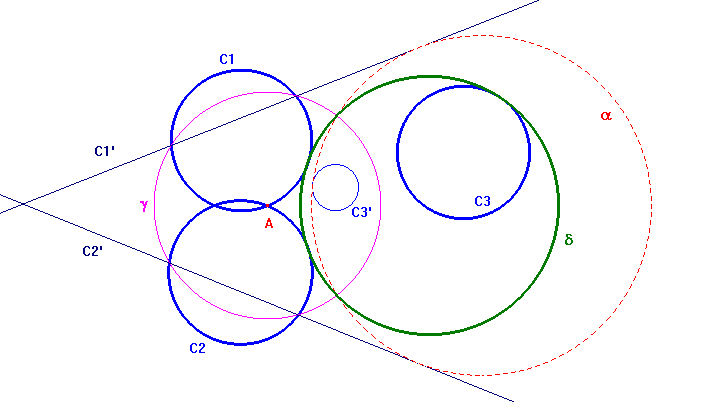
Cominciamo a considerare il caso, più semplice, in cui almeno due dei tre cerchi dati abbiano un punto in comune A. In questo caso si può considerare un'inversione di centro A e raggio qualunque: i due cerchi passanti per A si trasformano in rette, mentre l'altro cerchio si trasforma in un cerchio (o in una retta se passa anch'esso per A). Siamo ricondotti al caso di due rette e un cerchio o di tre rette. Per inversione si ritrovano le soluzioni richieste. Nella figura qui sotto C1, C2, C3 sono le tre circonferenze date, di cui due si incontrano in A. Con centro in A abbiamo considerato il circolo di inversione γ, le rette C1', C2', inverse di C1 e C2, e il cerchio C3', inverso di C3. La circonferenza α è una delle circonferenze tangenti a C1', C2', C3'. La circonferenza δ, ottenuta per inversione da α, è una delle circonferenze cercate.
Consideriamo ora il caso in cui due delle tre circonferenze siano concentriche (se lo fossero tutte e tre non ci sarebbero soluzioni), anche se la terza circonferenza incontra, come nella figura più sotto, una delle due. Perché il problema abbia soluzioni la terza circonferenza deve almeno "affacciarsi" nella corona circolare individuata dalle prime due.
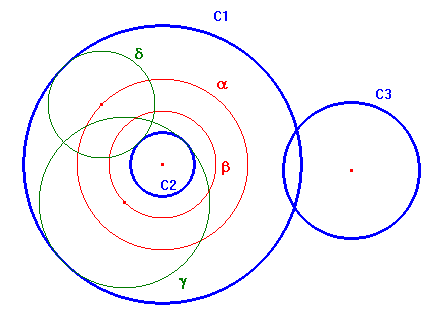
Nella figura di seguito C1, C2, C3 sono le tre circonferenze date. Le circonferenze cercate sono del tipo di γ e δ, cioè con diametro r1+r2 o r1-r2 e con centro sulle circonferenze α e β. Tra tutte queste circonferenze quelle tangenti anche a C3 si trovano con una costruzione elementare, come si può vedere nella figura qui sotto.
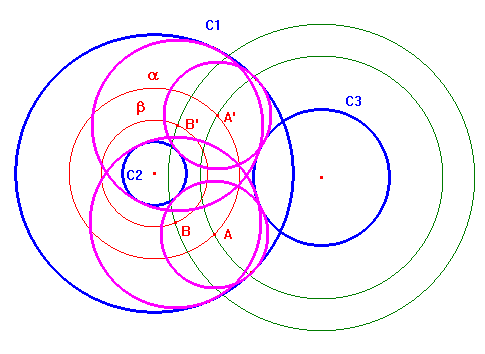
Basta costruire le circonferenze concentriche a C3 e di raggi r3+(r1+r2) oppure r3+(r1-r2) e considerare le loro intersezioni A, A', B, B', con le circonferenze α e β
E veniamo infine al caso generale, in cui le circonferenze non hanno punti in comune, e non ci sono due circonferenze concentriche. Ci si può ridurre al caso delle due circonferenze concentriche mediante una inversione di raggio qualunque e che abbia centro in uno dei due punti limite del fascio individuato da due delle tre circonferenze date.
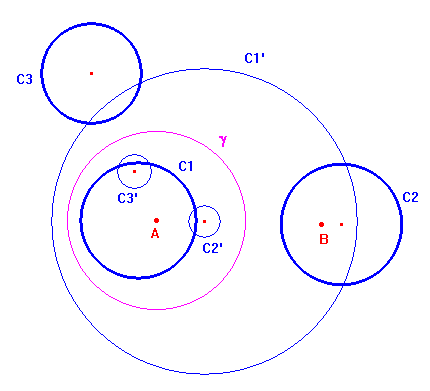
Nella figura qui sotto si vedono le tre circonferenze date, C1, C2, C3, i punti limite A e B del fascio individuato dalle circonferenze C1 e C2, il circolo di inversione γ e le tre circonferenze C1', C2', C3' inverse delle tre circonferenze date. Si è ricondotti al caso appena trattato di tre circonferenze di cui due concentriche.
Solo per il piacere degli occhi puoi vedere un'animazione della figura finale.