Le circonferenze per due punti e tangenti ad una circonferenza data
Sono dati due punti A e B ed una circonferenza γ di centro O e raggio r. Vogliamo costruire le circonferenze passanti per A e B e tangenti alla circonferenza data.
Proponiamo due costruzioni diverse nella forma ma identiche nella sostanza, la prima basata sull'asse radicale di due circonferenze e il centro radicale di tre circonferenze, la seconda basta sulle proprietà dei fasci di circoli. Proponiamo poi una terza costruzione, basata invece sull'inversione, e quindi sostanzialmente diversa dalle precedenti.
Prima costruzione
L'idea della costruzione è molto semplice. Considerati i due punti A e B e la circonferenza γ, si tracci una qualunque circonferenza, δ, passante per A e B ed intersecante γ in due punti R ed S . Indichiamo inoltre con η una delle circonferenze cercate. La retta r passante per A e B è asse radicale di δ ed η, la retta s passante per R ed S è asse radicale di γ e δ, per cui Q è centro radicale delle tre circonferenze. Se ne deduce che l'asse radicale di γ ed η deve passare per Q; tale asse radicale deve inoltre essere tangente a γ (la circonferenza incognita e γ devono essere tangenti!): basterà allora condurre da Q le tangenti a γ. Detti T1 e T2 i due punti di tangenza si possono costruire due circonferenze che soddisfano alla richiesta del problema, una per A, B e T1, l'altra per A, B e T2. E' chiaro che il problema non ha soluzioni se i due punti sono uno interno ed uno esterno a γ, è banale se i due punti stanno entrambi su γ, richiede qualche considerazione particolare se r ed s sono parallele, cioè se l'asse di AB passa per O (nel qual caso il punto Q non esiste) e se uno dei due punti sta su γ.
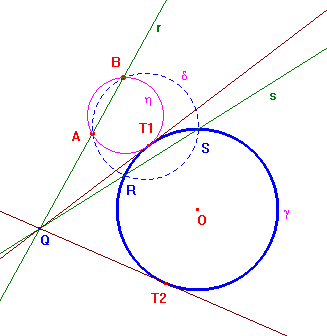
Si vedano le costruzioni relative ai vari casi, selezionandole dall'elenco.
- Punti esterni
- Punti interni
- Punti esterni, caso particolare
- Un punto sulla circonferenza
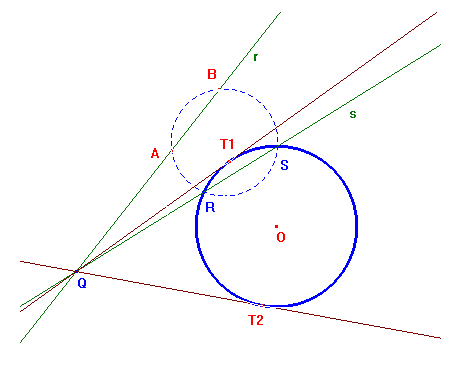
Seconda costruzione
Ci riferiamo solo al caso in cui i punti dati sono esterni al circolo, con l'asse di AB non passante per O. Bastano pochi adattamenti per gli altri casi. Come si vede dalla discussione che segue, solo l'impostazione formale è diversa dalla precedente, in realtà la costruzione è identica.
Siano dati i due punti A e B e la circonferenza di centro O. I circoli che cerchiamo fanno parte del fascio di punti base A e B. I punti di tangenza T1 e T2 con il circolo di centro O, sufficienti a determinare questi circoli, sono le intersezioni del circolo di centro O e del circolo ad esso ortogonale appartenente al fascio di punti limite A e B (coniugato del fascio di punti base A e B). Per trovare questo circolo basta prendere un qualunque circolo di centro M per A e B e trovare l'asse radicale di quest'ultimo e del circolo dato: la sua intersezione L con la retta AB ne è il centro. Il raggio si trova conducendo da L le tangenti al circolo dato. Come si vede si tratta in sostanza della stessa costruzione di prima. Puoi vedere un'animazione che mostra come la scelta di M sia ininfluente ai fini della costruzione.
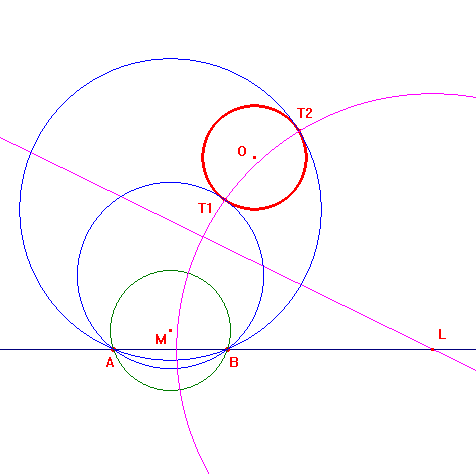
Terza costruzione
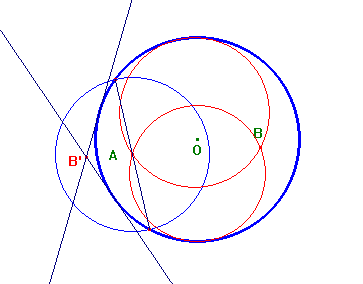
Dati i due punti A e B e il cerchio O, consideriamo l'inversione di centro A che lascia invariato il cerchio O (cioè tale che il cerchio O sia anallagmatico per questa inversione. Tale inversione si ottiene in maniera diversa a seconda che il punto A sia interno o esterno al cerchio O. Se dal punto B', omologo di B nell'inversione suddetta, si conducono le tangenti al cerchio O, i loro cerchi inversi nella predetta inversione sono i cerchi richiesti. Si vedano le costruzioni nei due casi citati nelle figure qui sotto. Si osservi che entrambe le costruzioni sono possibili solo se B è interno od esterno al cerchio O allo stesso modo di A.
A e B sono esterni al cerchio O. In questo caso l'inversione
che lascia invariato il cerchio O è un'inversione
positiva e il cerchio di inversione è il cerchio di
centro A e ortogonale al cerchio O.
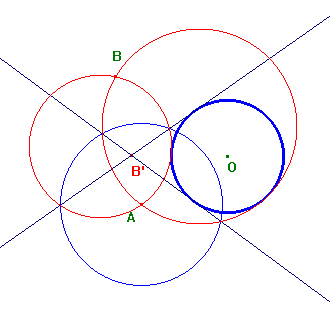
A e B sono interni al cerchio O. In questo caso l'inversione cercata è un 'inversione negativa, che può essere considerata prodotto tra un'inversione positiva e una simmetria centrale di centro A. L'inversione positiva ha come cerchio di inversione il cerchio di centro A che è tagliato diametralmente dal cerchio O.
Si veda un'animazione con CabriJava, costruita usando l'inversione.