Superficie di un solido di rotazione

Con una tecnica molto simile a quella utilizzata per il calcolo della lunghezza di un arco di curva, si può ricavare anche la superficie laterale di un solido di rotazione, ottenuto ruotando di 360° attorno all'asse delle ascisse un trapezoide.

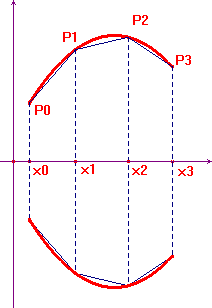
Considerata una funzione f derivabile in un intervallo [a,b] e positiva, e la spezzata individuata sul suo grafico da una suddivisione dell'intervallo [a,b], la superficie del solido ottenuto da una rotazione completa attorno all'asse delle x del trapezoide individuato dalla funzione può essere approssimata con la superficie ottenuta dalla rotazione della spezzata (purché i suoi lati siano "infinitamente piccoli"). Ciascun lato della spezzata, per rotazione, produce la superficie laterale di un tronco di cono, la cui area è la lunghezza del lato della spezzata per la lunghezza della circonferenza descritta dal punto medio del lato. L'area totale sarà: . Applicando il teorema di Lagrange e osservando che il punto medio di ciascun lato va a coincidere con gli estremi, al tendere a zero della lunghezza dei lati, si ottiene facilmente: . Se la funzione fosse negativa (magari a tratti), basterebbe prenderne il modulo all'interno dell'integrale.

Naturalmente anche questa formula è di solito di difficile applicazione, in quanto l'integrale richiesto spesso non è elementarmente calcolabile.