Volume di un solido di rotazione
Consideriamo la funzione f(x)=x/2 e il trapezoide (in questo caso un triangolo) da essa individuato tra l'origine e un punto b. Per calcolare l'integrale possiamo considerare le somme di Cauchy relative ad una particolare suddivisione dell'intervallo [a,b], in parti "infinitamente piccole" dx, ciascuna delle quali avrà un'altezza f(x).
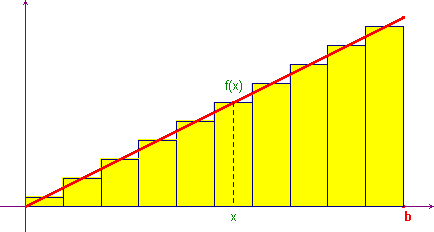
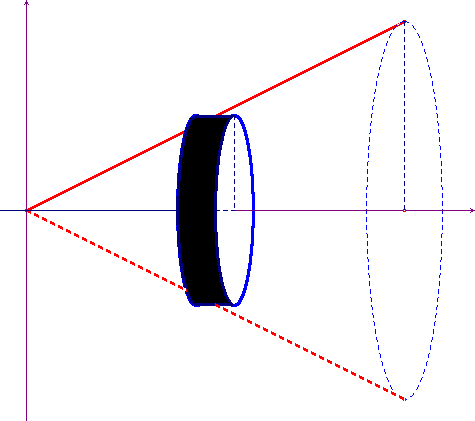
Immaginiamo ora di far ruotare il trapezoide attorno all'asse delle ascisse, di
un giro completo, ottenendo un solido di rotazione (in questo caso un cono). Ciascuno dei
rettangoli della somma di Cauchy genera un cilindro di altezza dx e di raggio di base
f(x): il volume di questi cilindri sarà allora 
. Nello stesso modo in cui abbiamo concluso che l'area del
trapezoide è 
, potremo concludere che il volume del solido di rotazione è 
. Si può facilmente
controllare la bontà di questo risultato nel caso particolare del cono rappresentato qui
di seguito.
Esempio
Calcolare il volume del solido ottenuto da una rotazione completa attorno all'asse delle
ascisse del dominio piano limitato dal grafico della funzione 
, dall'asse delle ascisse e dalle rette
x=0,
x=4.
.
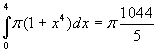Si osservi che l'area del trapezoide individuato dal grafico della funzione e dall'asse
delle ascisse non è elementarmente calcolabile in quanto la funzione non è elementarmente
integrabile.
