Metodi per la ricerca degli asintoti
Asintoti verticali.
La ricerca degli asintoti verticali si fa, secondo la
definizione, determinando i punti per cui la funzione ha limite
infinito. Tale ricerca, nei casi che ci interessano, si
deduce facilmente dal dominio della funzione e da semplici
considerazioni, come si vedrà negli esempi che seguono.
Ricordiamo che, come già osservato, una funzione
può avere infiniti asintoti verticali: un esempio tra le
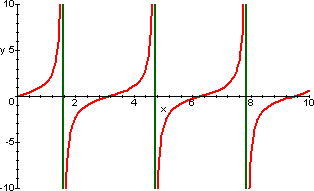
funzioni elementari è fornito da y=tgx
, che ha per asintoti tutte le rette 
.
Per l'esistenza di un asintoto verticale non è
necessario che la funzione abbia un denominatore che si annulla
per x=c, come risulta per esempio dalla considerazione
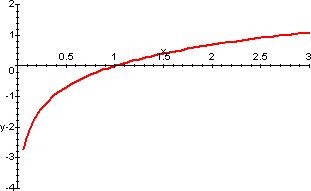
della funzione y=lnx
che ha come asintoto verticale la retta x=0, nonostante
non abbia alcun denominatore; inoltre non è nemmeno
sufficiente che la funzione abbia un denominatore che si
annulla, come risulta per esempio dalla considerazione della
funzione 
, che non ha per asintoto verticale la
retta x=0, nonostante il suo denominatore si annulli in
corrispondenza di 0. Quest'ultima osservazione è da
tenere presente anche nel caso delle funzioni razionali fratte
(quozienti di polinomi), come è provato dalla funzione
, che non ha asintoti verticali, nonostante il
denominatore si annulli in corrispondenza di 1.
Asintoti orizzontali.
Ci riferiremo alle funzioni definite in un intorno di +∞,
le considerazioni per le funzioni definite in un intorno di
-∞ sono analoghe. La ricerca di questi asintoti si fa
calcolando il limite della funzione, per 
: se questo limite esiste finito, diciamolo k, allora in
base alla definizione la retta y=k è un asintoto
orizzontale. Se il limite non esiste o vale ∞ (con o senza
segno) non ci sono asintoti orizzontali. Come già detto
l'esistenza dell'asintoto orizzontale preclude
l'esistenza dell'asintoto obliquo.
Asintoti obliqui.
Sempre con riferimento alle funzioni definite in un intorno di
+∞, se il limite considerato nel caso precedente non
esiste, non ci sono nemmeno asintoti obliqui. se invece esso
è infinito si può osservare quanto segue. Siano m
e q due numeri reali, con m≠0, e si osservi che 
; se il primo membro, per , deve avere per limite zero, è necessario che la
quantità tra parentesi graffe abbia per limite zero;
questo è possibile solo se 
, in quanto 
. Se ora , allora f(x)-mx deve avere per limite
q, in quanto f(x)-mx-q deve avere per limite
zero. Se ne deduce che y=mx+q è un asintoto
obliquo solo se 
. E' immediato che se,
viceversa, 
, allora la retta
y=mx+q è un asintoto obliquo.
Schema per la ricerca (asintoti orizzontali ed obliqui)
Considerato il caso , il seguente schema
indica come procedere operativamente per la ricerca degli
asintoti orizzontali ed obliqui:
Per il caso di -∞ si procede in maniera perfettamente analoga.
Riportiamo ora alcuni esempi che si riferiscono ad ognuno dei casi contemplati nello schema sopra riportato, nello stesso ordine (tutti i limiti si intendono a +∞).
a) La funzione
f(x)=sinx non ha limite, dunque non ha asintoti
orizzontali od obliqui.
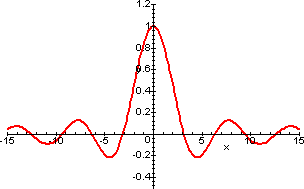
b) La funzione
ha per limite 1, dunque y=1 è asintoto
orizzontale.
c) La funzione f(x)=x(sinx+2) tende a +∞, ma f(x)/x non ha limiti, dunque non ci sono asintoti.
d) La funzione f(x)=ex tende a +∞ (niente asintoti orizzontali), ma f(x)/x tende a +∞, dunque non ci sono nemmeno asintoti obliqui.
e) La funzione f(x)=lnx tende a +∞ (niente asintoti orizzontali), ma f(x)/x tende a zero, dunque non ci sono nemmeno asintoti obliqui.
f) La funzione f(x)=x+sinx tende a +∞ (niente asintoti orizzontali), f(x)/x tende a 1, ma f(x)-mx non ha limite, dunque non ci sono nemmeno asintoti obliqui.
g) La funzione
tende a +∞ (niente
asintoti orizzontali), f(x)/x tende a 1, ma
f(x)-mx tende a +∞, dunque non ci sono nemmeno
asintoti obliqui.
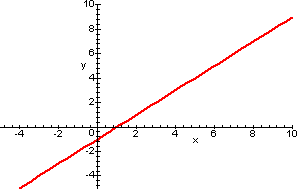
h) La funzione
tende a +∞ (niente
asintoti orizzontali), f(x)/x tende a 1,
f(x)-mx tende a 1, dunque la retta y=x+1 è asintoto obliquo.