Qualche altro esempio classico
Oltre ai due esempi che abbiamo diffusamente trattato in questa monografia, ci sono alcune altre figure classiche, generate con procedimenti molti simili a quelli che abbiamo considerato, e che vale la pena di ricordare. Naturalmente le possibilità sono infinite e qui ricorderemo solo alcuni dei casi che hanno fatto storia.
1 - Il triangolo (o setaccio) di Sierpinski.
Questo frattale fu introdotto dal topologo polacco Waclaw Sierpinski nel 1915 e ha conosciuto una enorme popolarità. Si parte da un triangolo equilatero, da cui si sopprime. Nella figura qui sotto sono rappresentati i primi tre passi nella costruzione.
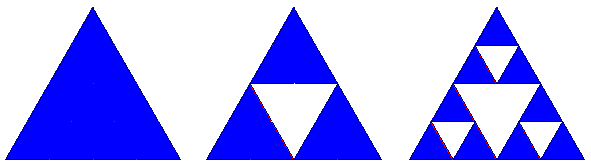
E' facile calcolare la sua dimensione di
autosimilarità: se si riduce la scala di 1/2 si ottengono
tre figure simili alla data, per cui la dimensione è
log3/log2≈1.5850. Immaginiamo che il triangolo dato sia
rappresentato in un sistema cartesiano ortogonale con i vertici
in (0,0), (1,0) e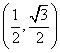 
rispettivamente.
Consideriamo poi un'omotetia di centro l'origine e
rapporto di omotetia 1/2, 
, e la stessa omotetia composta con due traslazioni,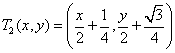 
e 
. E' evidente che la
figura richiesta può essere ottenuta mediante
applicazione successiva di queste tre trasformazioni, o, in
altre parole, che il triangolo S di Sierpinski è
l'unica figura del piano tale che S=T(S), ove
T=T1
T2T3. L'interesse di questa figura
è che è ottenuta a partire da una superficie
anziché da un segmento. Anche per essa si possono
ripetere considerazioni simili a quelle fatte per l'insieme
di Cantor: per esempio la superficie rimasta alla fine
è chiaramente nulla, anche se ogni volta si toglie solo
un quarto dell'area, lasciandone tre quarti. La sua
dimensione è appena un po' più vicina a quella
di una superficie (2) che a quella di una linea (1), e quindi
è molto di più, dimensionalmente, che non il
merletto di Koch.
2 - La spugna di Menger.
Si prende un cubo e lo si divide in 27 cubi di lato 1/3 dell'originario; a questo punto si sopprime il cubo centrale e i sei cubi che stanno al centro delle facce, cioè 7 cubi in tutto. rimanendo con 20 cubi. Si ripete il procedimento su ognuno dei cubi rimasti. Anche in questo caso è facile calcolare la dimensione di autosimilarità, basta osservare che riducendo ad un terzo le dimensioni originali si ottengono 20 copie della figura: la dimensione frattale è dunque log20/log3≈2,727. Poiché è più vicina a tre che a due è più un solido che una superficie, anche se ha volume nullo!
3 - Insiemi di Cantor a misura positiva.
Riprendiamo in considerazione l'intervallo [0,1] e fissiamo un numero k, con 0<k<1. Immaginiamo di sopprimere, anziché l'intervallo centrale di ampiezza 1/3, l'intervallo centrale di ampiezza k/2. Ripetiamo poi il procedimento sopprimendo, da ciascuno dei due intervalli rimasti, la parte centrale di ampiezza k/8, in modo che il totale delle parti rimasse diventi k/2+k/4. Ripetiamo di nuovo il procedimento, sopprimendo da ciascuno dei 4 intervalli rimasti la parte centrale di ampiezza k/32, portando la lunghezza totale soppressa a k/2+k/4+k/8. Ripetendo all'infinito questo procedimento sopprimeremo una unione di segmenti aventi lunghezza totale k: la parte rimasta avrà dunque lunghezza 1-k. Ciascuno degli insiemi così ottenuti si chiama un insieme di Cantor a misura positiva. Per essi la dimensione di Hausdorff-Besicovitch è 1, cioè coincidente con la dimensione topologica, e dunque, strettamente parlando, non si tratta di frattali. Ciò nonostante anche questi insiemi sono perfetti e ovunque non densi, cioè non esiste alcun intervallo di reali contenuto in essi. Si può provare che tutti questi insiemi sono tra di loro omeomorfi.
4 - Costruzione di curve di assegnata dimensione.
Limitandoci a situazioni semplici, vogliamo mostrare come si
possa costruire con un procedimento di iterazioni successive,
curve di dimensione assegnata. Se per esempio cerchiamo una
curva di dimensione 3/2, potremo operare in modo da ottenere
. Si può prendere 
e fare in modo che N=8. Un modo per farlo
è:
.
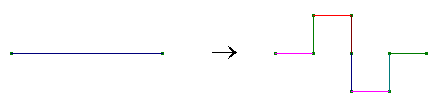Un ulteriore esempio si ha con la costruzione seguente, dove
N=4 e 
. Si ha D=4/3.
.
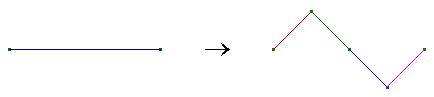