La dimensione di Hausdorff-Besicovitch
Il concetto di dimensione per le figure dello spazio, che vogliamo introdurre in questa pagina, è quella ritenuta più adatta a descrivere il maggior numero di situazioni di interesse della geometria frattale, tanto che Benoit Mandelbrot, nel suo libro The Fractal Geometry of Nature, W.H.Freeman and Co., N.Y. 1977, dà la seguente definizione di frattale:
Un frattale è, per definizione, un
insieme per il quale la dimensione di Hausdorff-Besicovitch
è strettamente più grande della dimensione
topologica.
Purtroppo questa definizione non è semplice e anche per questo motivo abbiamo preferito introdurre prima altre tecniche per valutare caratteristiche degli insiemi che la dimensione topologica non riesce a distinguere. Purtroppo è da segnalare che, anche se non ci sono risultati definitivi, la definizione di dimensione per esempio per autosimilarità non è certo che porti sempre (quando applicabile) allo stesso numero che si ottiene con la definizione di Hausdorff-Besicovitch: è noto che dHB≤dsim, e che, di solito, dHB=dsim, ma non sono noti criteri a priori per stabilire quando questo succede. Inoltre il calcolo effettivo della dimensione di Hausdorff-Besicovitch risulta molto complesso ed è poco usato nella pratica: per questo ci limiteremo solo ad un cenno introduttivo. Nelle cose che diremo si ritrovano alcune delle tecniche che abbiamo già visto parlando di autosimilarità, box counting o compass dimension.
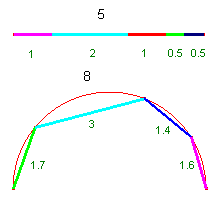Per capire il metodo che utilizzeremo
cominciamo a considerare un segmento AB di lunghezza L
e supponiamo di volerlo ricoprire con dei regoli di lunghezza
massima s. Se indichiamo con si la
lunghezza di ciascuno dei regoli, la lunghezza del segmento
sarà chiaramente 
. Se variamo la
massima lunghezza consentita per i regoli non cambia nulla e
potremmo anche considerare il limite, quando s tende a
zero, della somma precedente, come lunghezza del segmento: 
. Se invece di misurare un segmento vogliamo
misurare una linea curva, per esempio una semicirconferenza,
allora la 
rappresenterebbe solo la
lunghezza approssimata della circonferenza, potremmo chiamarla
la lunghezza approssimata di ordine s, e la indicheremo
con Ls. Per avere la lunghezza
"esatta" dovremmo imporre che la massima
lunghezza dei regoli diventi sempre più piccola,
ottenendo la stessa formula valida per il segmento: 
.
Potremmo anche voler calcolare
l'area del segmento dato, basterebbe considerare
anziché segmenti si di massima
ampiezza s, quadrati con gli stessi lati. L'area
totale occupata dai quadrati sarebbe 
e risulta evidente che, se facciamo tendere a zero la massima
lunghezza dei regoli, il limite a cui tende quest'area
sarà zero (meno male!): la figura, man mano che
s tende a zero, tende sempre di più ad
avvicinarsi ad un rettangolo di base L ed altezza zero.
Potremmo porre, in perfetta analogia con il caso della
lunghezza: 
. E' abbastanza
evidente che, anche nel caso della semicirconferenza, avremmo
ottenuto A=0.
Se, a questo punto, volessimo calcolare il volume del segmento o
della semicirconferenza dovremmo usare dei cubetti di lato
si e otterremmo, con evidente significato
dei simboli: 
.
Le tre formule ottenute per la lunghezza, l'area e il volume
hanno la stessa forma e potremmo unificarle con opportuni
simboli. Si usa chiamare L misura unidimensionale,
A misura bidimensionale, V misura
tridimensionale del segmento e si scrive M1,
M2, M3, nei tre casi. Se
si osserva che 1, 2, 3 sono gli esponenti di
si nelle tre formule, indicando
genericamente con D questi esponenti, e con E
l'oggetto (segmento o circonferenza) da misurare, le tre
formule possono essere scritte in maniera compatta così:
.
A questo punto possiamo guardare la formula ottenuta con
un'altra ottica. Sappiamo che se in essa mettiamo D=1
otteniamo la lunghezza della curva, se mettiamo D=2 o D=3
otteniamo zero. Proviamo a chiederci: che cosa otterremmo se
mettessimo D=0.9 oppure D=1.1? Per rendercene conto facciamo
riferimento al caso del segmento e supponiamo di prendere, per
semplicità, i segmenti si tutti
uguali alla massima ampiezza consentita: s. Si ha
allora: 
. Se D=0.9 si ottiene:
e quindi 
(il numeratore vale costantemente L e il denominatore
tende na diventare sempre più piccolo. Se si prende D=1.1
si trova invece, con la stessa tecnica, 
. Anzi tale limite vale +∞ per tutti i valori
positivi di D minori di 1, vale 0 per tutti i valori
maggiori di 1. Possiamo dunque interpretare D come
quell'unico esponente che, posto nella formula 
, fa si che il limite non tenda né a zero
né a +∞. Non sarebbe difficile provare che questo
ragionamento funziona anche se prendiamo segmenti di ampiezza
diversa.
Abitualmente si usa indicare con Ai i vari segmenti o quadrati o cubetti e con diam(Ai) la loro dimensione lineare. Dunque i risultati sopra ottenuti per un segmento e per una circonferenza, e immediatamente estendibili ad una qualunque linea piana normale, si possono compendiare nella formula:
(**).
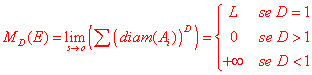Il valore D=1 si presenta cioè come un valore cruciale al disotto del quale il limite diverge, mentre al disopra il limite diventa zero.
Non è a questo punto difficile provare che se consideriamo un quadrato (o più in generale una normale superficie piana) otterremo la stessa formula (**), con valore cruciale per D uguale a 2, per il quale si ottiene l'area della superficie. Per un cubo o un normale solido dello spazio euclideo si ottiene ancora la stessa formula con valore cruciale per D uguale a tre, per il quale si ottiene il volume del solido.
Ci possiamo chiedere a questo punto: che cosa succede per situazioni patologiche come l'insieme di Cantor o il merletto di Koch?. Non ci vuole molto a convincersi, rivedendo quanto è stato finora in questa monografia, che si ottiene:
-
Per l'insieme di Cantor
;
-
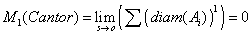Per il merletto di Koch
.
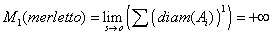formule che non sono altro che l'espressione del fatto che l''insieme di Cantor ha lunghezza nulla, il merletto di Koch infinita.
In analogia con quello che abbiamo fatto altre volte ci viene il sospetto che si possa cercare di seguire un'altra strada, e precisamente quella di andare a vedere se esiste per caso un qualche valore di D che abbia un ruolo cruciale come succede per le figure normali, magari rinunciando al fatto che il limite in questione rappresenti la lunghezza, l'area o il volume dell'oggetto.
La risposta è affermativa, anche se è necessaria qualche precisazione, ed è addirittura valida per tutti gli insiemi dello spazio (in realtà è valida negli spazi metrici, ma questo esula dagli scopi del nostro sito...). Si procede, generalizzando quanto finora detto, ma sempre rimanendo ad un livello abbastanza informale, nel seguente modo:
Dato un insieme A dello
spazio (o più in generale di uno spazio metrico) si
considera un ricoprimento di A con insiemi
Ai di diametro non superiore ad un
determinato valore s. Si fissa poi un numero positivo
D e si considera la somma dei diametri di tutti questi
insiemi, elevati al valore scelto D: fissato s
ci sono infinite somme possibili, a seconda del diametro
effettivo che si prende e anche a seconda di come si dispongono
gli insiemi Ai. Si considera l'estremo
inferiore di tutte queste possibili somme (cioè in
sostanza si prende il ricoprimento più efficiente e meno
dispendioso): tale insieme si chiama misura D-dimensionale
s-approssimata di Hausdorff dell'insieme A, 
. Si fa poi il limite di questa misura approssimata, al
tendere a zero di s, 
, limite che prende il nome di misura D-dimensionale
di Hausdorff dell'insieme A. Qualunque sia
l'insieme A esiste un unico valore, che indichiamo
con dimH(A), di D tale che per
D<dimH(A) tale misura è infinita,
mentre per D>dimH(A) tale misura è
0. Per D=dimH(A) tale misura può
essere finita oppure no e può coincidere oppure no con la
misura (lunghezza, area, volume) tradizionale dell'insieme.
Il numero dimH(A) si chiama dimensione di
Hausdorff-Besicovith
dell'insieme A in questione.
La misura e la dimensione così definite godono di proprietà molto interessanti, alcune delle quali segnaliamo esplicitamente:
- Se un insieme ha una certa misura D-dimensionale, e lo si scala di un fattore r mediante una similitudine, la misura del nuovo insieme si ottiene da quella dell'insieme originario moltiplicandola per rD.
-
Se A
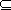B, sono due insiemi, si ha
dimH(A)≤dimH(B).
-
Gli insiemi con cardinalità
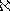0 hanno dimensione zero.
- Gli insiemi aperti hanno la dimensione giusta (in particolare i segmenti hanno dimensione 1, i quadrati 2, i cubi 3).
Non ci vuole molto (anche se il calcolo esplicito non è
banale), a questo punto, a capire che valgono i seguenti
risultati per due nostre vecchie conoscenze: 
e 
.