Il concetto di dimensione
Il Libro I degli Elementi di Euclide si apre con le seguenti definizioni:
- Definizione 1: Il punto è ciò che non ha parti.
- Definizione 2: Una linea è lunghezza senza senza larghezza.
- Definizione 3: Gli estremi di una linea sono punti.
- Definizione 4: Una linea retta è una linea che giace in modo uguale rispetto ai suoi punti.
- Definizione 5: Una superficie è ciò che ha solo lunghezza e larghezza.
- Definizione 6: I bordi di una superficie sono linee.
- Definizione 7: Una superficie piana è una superficie che giace in modo uguale rispetto alle sue rette.
Successivamente, quando passa alla geometria solida, Euclide apre il Libro XI con le seguenti definizioni:
- Definizione 1: Un solido è ciò che ha lunghezza, larghezza e profondità.
- Definizione 2: La faccia di un solido è una superficie.
In queste righe del più famoso e più utilizzato libro di matematica di tutti i tempi è contenuto il concetto di ciò che si intende con dimensione euclidea. L'intento di Euclide è di costruire una teoria assiomatica della geometria e, coerentemente, inizia con un elenco dei termini che saranno utilizzati e che vengono considerati concetti primitivi. Le descrizioni che accompagnano i termini che sono elencati non vengono mai utilizzate nel testo e hanno solo la funzione di "orientare" il lettore. Il significato di questi termini primitivi non sta nella breve descrizione che li accompagna, ma nelle proprietà che vengono successivamente assunte come assiomi. Per esempio il Primo postulato (E' possibile condurre una linea retta tra un qualsiasi punto e un qualsiasi altro punto) comincia a precisare il significato della parola punto che viene introdotta nella Definizione 1. Gli altri postulati e i teoremi che ne seguiranno preciseranno il significato di tutte le parole elencate in queste definizioni.
Nonostante questa limitazione non si può non notare che queste righe elencano quelle che sono le caratteristiche del concetto intuitivo di dimensione che tutti noi possediamo: il punto ha dimensione zero, la retta ha dimensione uno, il piano ha dimensione due, lo spazio ha dimensione tre. Il fatto che la retta abbia dimensione uno è "caratterizzato" dal fatto che i bordi delle sue parti (segmenti) sono punti (cioè oggetti di dimensione zero) e che i punti (cioè sempre oggetti di dimensione zero) sono in grado di spezzare le rette. Il piano ha dimensione due perché le sue parti (superfici) hanno bordi di dimensione 1 e perché le rette (che sono di dimensione 1) lo spezzano in due. Analogo discorso per lo spazio. Questa idea intuitiva di dimensione non fu sostanzialmente messa in discussione fino ai primi anni del 1900, quando Poincarè, tra le tante cose che era solito fare, pose l'attenzione sulla necessità di un'analisi più approfondita del concetto di dimensionalità.
Il concetto di dimensione si è venuto via via precisando successivamente e ha assunto oggi una forma molto più precisa di quanto non fosse in Euclide: si è pervenuti al concetto di dimensione topologica. Anche se qui non vogliamo occuparci in dettaglio di questo difficile problema, segnaliamo che la proprietà essenziale è che la dimensione topologica di una figura non si modifica se essa viene sottoposta a deformazioni continue (sostanzialmente piegamenti e stiramenti, ma senza strappi), in termini tecnici a deformazioni omeomorfiche. Uno dei fatti più interessanti della teoria delle dimensioni, è un teorema, dovuto a Lebesgue e a Brower, che caratterizza le dimensioni di una figura qualsiasi, tanto che da alcuni la proprietà enunciata nel teorema viene assunta come definizione di dimensione.
In termini molto elementari il contenuto di questo teorema può essere presentato come segue. Si consideri una semplice figura, per esempio a due dimensioni nel piano, e si supponga di ricoprirla con regioni sufficientemente piccole (si immagina che ciascuna contenga il proprio contorno). Allora qualunque sia la forma delle regioni piccole, ci saranno necessariamente dei punti in cui si incontrano tre o più di queste regioni. Inoltre esisteranno suddivisioni in cui ogni punto della figura appartiene al massimo a tre regioni. La cosa interessante è che il numero tre è esattamente di una unità superiore alle dimensioni della figura.
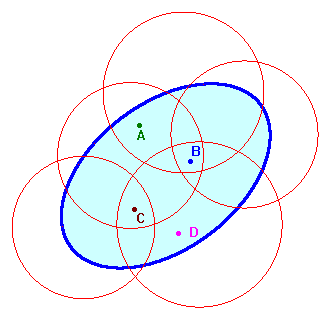Se si esamina la figura qui a fianco, in
cui abbiamo ricoperto la regione racchiusa dall'ellisse con
cerchi, si osserva che:
- Il punto A appartiene a due cerchi.
- Il punto B appartiene a quattro cerchi.
- Il punto C appartiene a tre cerchi.
-
Il punto D appartiene a un solo cerchio.
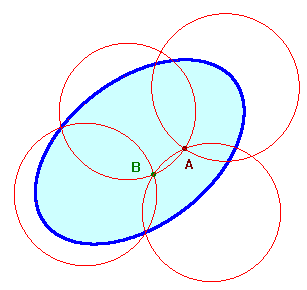Il ricoprimento qui a fianco, che si
riferisce alla stessa regione di sopra, è fatto in modo
che nessun punto appartiene a più di tre regioni. Solo i
punti A e B appartengono a tre regioni, gli altri al massimo a
due.
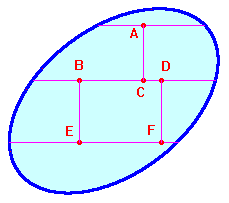Anche se si considera un ricoprimento più
regolare, come quello della figura qui a fianco, non si
può sperare di ricoprire la regione in modo che i punti
appartengano al massimo a due regioni: qui a fianco i punti A,
B, C, D, E, F appartengono a tre regioni, gli altri a due. Il
ricoprimento qui a fianco ricorda una pavimentazione con
mattonelle: per questo motivo questo problema si chiama anche
problema delle mattonelle.
Se invece di una regione bidimensionale consideriamo una linea, cioè una regione a una dimensione, possiamo osservare che un qualunque ricoprimento con regioni sufficientemente piccole potrà prevedere punti comuni anche a più di due regioni, e ci saranno ricoprimenti con punti comuni al massimo a due regioni, ma nessun ricoprimento sarà possibile che non preveda punti comuni ad almeno due regioni.
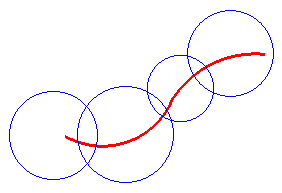Nel caso della linea rossa della figura qui a fianco il
ricoprimento indicato prevede punti comuni al massimo a due
regioni, e non si può scendere al di sotto di due: da
questo segue che la linea ha una dimensione.
Seguendo la falsariga di questi esempi enunciamo il teorema di Brower-Lebesgue relativo alla dimensione topologica di una figura:
Se una
figura a n dimensioni è coperta in modo
qualsiasi da regioni parziali sufficientemente piccole,
esisteranno punti appartenenti ad almeno n+1 di queste
regioni; inoltre è sempre possibile ricoprire la figura
con regioni arbitrariamente piccole, in modo che nessun punto
appartenga a più di n+1 regioni. La
proprietà enunciata è caratteristica
delle figure a n dimensioni.
Proviamo ad applicare questa tecnica all'insieme di Cantor: è chiaro che l'insieme può tranquillamente essere ricoperto da regioni circolari piccole quanto si vuole che siano completamente disgiunte, cioè con punti appartenenti al massimo a una regione. Per questo motivo la dimensione topologica dell'insieme di Cantor è zero.
Non ci vuole molto a provare, nello stesso modo, che il merletto di Koch ha invece dimensione topologica uno.
In ragione di questo teorema la dimensione topologica si può anche chiamare dimensione di Brower-Lebesgue o dimensione di ricoprimento (cover dimension).