Figure autosimili
E' noto dalla geometria elementare il concetto di similitudine tra due figure: in sostanza due figure si dicono simili se l'ingrandimento di una è esattamente sovrapponibile all'altra (eventualmente con traslazioni, rotazioni o riflessioni speculari).
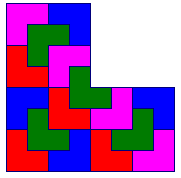
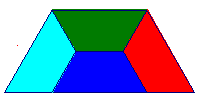
Esaminiamo ora le due figure qui sotto: si vede a colpo d'occhio che ciascuna di esse è costituita da parti simili tra loro e simili all'originale.
 .
.
Si usa dire che figure come queste hanno un certo grado di autosimilarità .
Se riprendiamo in esame l'insieme di Cantor possiamo notare come questa autosimilarità sia perfetta: l'insieme C è composto da due parti che sono copie identiche di C, in scala ridotta di 1/3; a sua volta ciascuna di queste due parti è costituita da due parti che sono copie identiche di C, ulteriormente ridotte di 1/3, e così via, all'infinito. Si noti che gli insiemi Cn, non godono della stessa proprietà, in quanto, come già osservato, Cn+1 è costituito da due copie, ridotte di 1/3, di Cn e non di se stesso.
Figure che godono della proprietà ora indicata per l'insieme di Cantor si dicono autosimili. Anche il merletto di Koch e il fiocco di neve di Koch sono autosimili. Si può chiamare questa proprietà anche invarianza rispetto al cambiamento di scala: se si esaminano questi oggetti a scale diverse si incontrano sempre gli stessi elementi fondamentali.
Naturalmente una autosimilarità perfetta si manifesta anche in un segmento, in un quadrato, in un cubo. Ogni segmento si può pensare costituito da due (o tre, o quattro, ecc.) copie identiche di se stesso, e questo ad ogni livello. Parimenti un quadrato si può considerare costituito da quattro (o nove, o sedici, ecc.) copie esatte di se stesso, mentre un cubo da otto (o ventisette, o sessantaquattro, ecc.) copie di se stesso, sempre ad ogni livello.
Le figure autosimili come l'insieme di Cantor o il merletto di Koch sono molto interessanti. Per esempio il merletto di Koch ha una proprietà che lo rende radicalmente diverso dalle "usuali" curve, e non tanto per il fatto che ha lunghezza infinita. L'idea fondamentale su cui si basa lo studio delle curve mediante il calcolo differenziale è quella di trasformare le curve in segmenti, in modo da potervi applicare i concetti tipici delle linee rette (per esempio la pendenza). Leibnitz asserì esplicitamente che tutte le curve sono costituite da segmenti infinitamente piccoli, chiamati, seppur impropriamente, differenziali. E' chiaro che ci potevano essere dei punti eccezionali, ma quest'idea entrò proprio in crisi quando cominciarono ad essere descritte curve che non hanno tangenti in alcun punto. Il merletto di Koch rientra in questa categoria di curve che risultano essere "intrattabili" con i metodi basati sul concetto di tangente, proprio perché, anche se se ne esamina solo un pezzetto infinitesimo, la curva mantiene tutta la sua complessità, e non si approssima affatto ad una retta.
Un esempio oltremodo interessante di curva patologica è la cosiddetta curva di Weierstrass, che è derivabile solo su un insieme di misura nulla ed è il grafico di una funzione continua di R in R, mentre il merletto di Koch non è il grafico di una funzione.