Punti fissi e periodici
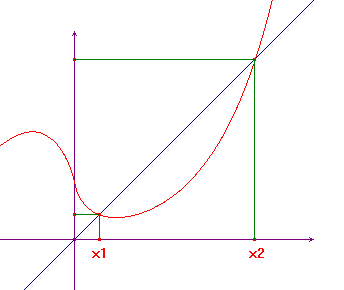Data una funzione 
, in cui A e B sono sottoinsiemi
di uno stesso insieme, un punto x0 di
A si dice fisso
se f(x0)=x0. Graficamente, per le
funzioni reali di variabile reale, si capisce subito che i punti
fissi si ottengono intersecando il grafico della funzione con la
bisettrice y=x. Nella figura qui a lato i punti x1 e x2
sono fissi. In termini di orbite un punto è fisso per una
funzione f se l'orbita del punto è una
successione costante. Per esempio il punto 1 è fisso per
la funzione f(x)=x2, il punto
0.739085... è fisso per la funzione f(x)=cosx.
Un punto si dice definitivamente
fisso se l'orbita del punto è costante da
un certo punto in poi. Per esempio il punto -1 è
definitivamente fisso per la funzione
f(x)=x2: si ha f(-1)=1, f(f(1)=1 e
d'ora in poi iterando la funzione si ottiene sempre 1.
Similmente π è definitivamente fisso per la funzione
f(x)=senx.
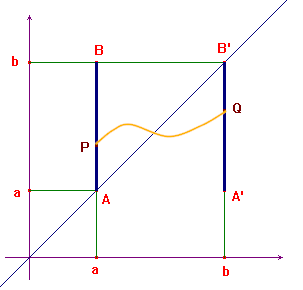Il concetto di
punto fisso è molto importante ed interviene in parecchi
teoremi di analisi (teorema del punto fisso di Brouwer, teorema
del punto fisso di Banach, ecc.).
Per quanto riguarda le funzioni reali di variabile reale il
teorema del punto fisso si può così
enunciare: se 
è una funzione
continua e se 
, allora g ha
almeno un punto fisso. Graficamente questo teorema è
abbastanza evidente: nelle condizioni dell'enunciato il
grafico della funzione g deve partire da un punto come
P del segmento AB e deve arrivare ad un punto come Q del
segmento A'B'; è chiaro che dovrà
intersecare la bisettrice y=x almeno una volta.
Per i limiti di successioni iterative vale il seguente:
Teorema: Sia A un sottoinsieme di R, f
una funzione di A in A, e k un elemento di A. Se la
successione iterativa a0=k,
an+1=f(an) converge al limite
l
A e la
funzione è continua in l, allora l
è un punto fisso per f.
Questa teorema, che è una semplice applicazione del concetto di funzione continua, é di grande aiuto nella ricerca dei limiti di questo tipo di successioni. Si osservi che il teorema non afferma nulla sulla esistenza del limite.
Consideriamo ora nuovamente la funzione f e indichiamo con f n la composta di f con se stessa n volte. La funzione f n ha ovviamente tutti gli eventuali punti fissi di f, ma può averne anche altri. Un punto x0 che sia fisso per f n, ma non per f n-1, si dice punto periodico, di periodo n, per f. Dal punto di vista delle orbite ciò significa che l'orbita di x0 ripassa periodicamente, ad intervalli regolari, per lo stesso valore. Per esempio il punto 3 è periodico, di periodo due, per la funzione f(x)=1/x (come già visto, ogni punto non nullo e diverso da ±1 gode della stessa proprietà).
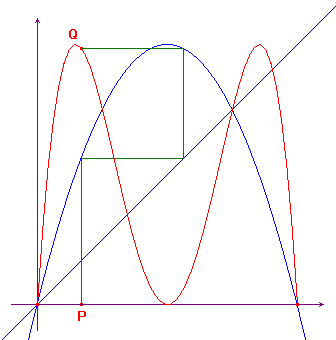Un esempio
interessante e di cui ci occuperemo ancora in seguito è
quello della funzione f(x)=4x(1-x). Nella figura a lato
è rappresentato il grafico di f e quello di
g=fof, costruito con
la tecnica grafica per la costruzione della funzione composta.
Si vede che la funzione g ha gli stessi punti fissi di
f, ma in aggiunta ne ha anche altri due. I punti fissi
di f sono facilmente ricavabili (perché
soluzioni di un'equazione di secondo grado) e sono 0 e 3/4.
I punti fissi di g sono soluzioni di un'equazione
di quarto grado, di cui però conosciamo già due
soluzioni: è allora facile trovare le altre due. Questi
due nuovi punti sono punti periodici di periodo due della
funzione f.
Puoi vedere un'animazione
di questa costruzione.
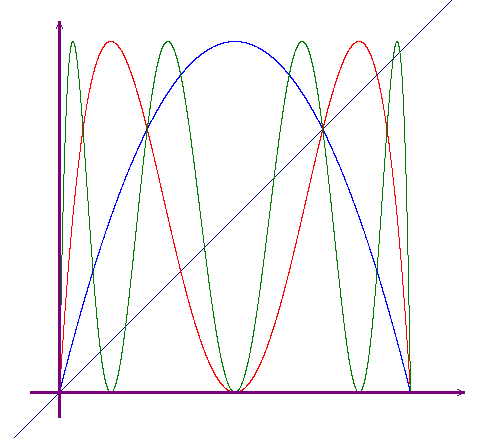La figura qui a lato
mostra, sempre relativamente alla funzione
f(x)=4x(1-x), anche il grafico di fofof (in verde): si nota la presenza di otto
punti fissi, di cui due coincidenti con quelli di f, e
sei nuovi. In questo caso non c'è speranza di
determinarli analiticamente in quanto dell'equazione
relativa (di ottavo grado) conosciamo due sole soluzioni e non
esistono regole generali per la determinazione delle sei
soluzioni rimanenti. I sei nuovi punti fissi di fofof saranno punti di periodo 3 per la
funzione f di partenza.
Si noti anche come, ovviamente, i punti fissi di fof non siano necessariamente anche
punti fissi di fofof,
mentre lo saranno di fofofof,
che si può pensare come (fof)o(fof).