Iterazioni e funzioni non lineari
E' chiaro che la costruzione di successioni con il metodo iterativo è possibile solo se f(an) sta sempre nel dominio di f, per ogni n, in modo da poter eseguire l'iterazione: la cosa è sicuramente possibile per le funzioni per cui l'immagine del dominio coincide con il dominio.
 Come
primo esempio di una funzione non lineare consideriamo la
funzione radice quadrata, che ha dominio e codominio coincidente
con i reali positivi. Dato k>0 poniamo
Come
primo esempio di una funzione non lineare consideriamo la
funzione radice quadrata, che ha dominio e codominio coincidente
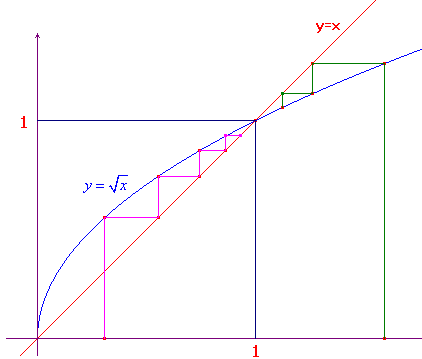
con i reali positivi. Dato k>0 poniamo 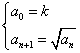 . La figura a lato è costruita a partire da due
diversi valori di k, uno maggiore e uno minore di 1:
è chiaro che, in entrambi i casi, la successione converge
ad 1. Se si fosse preso k=0, la successione sarebbe
rimasta stabilmente sullo zero.
. La figura a lato è costruita a partire da due
diversi valori di k, uno maggiore e uno minore di 1:
è chiaro che, in entrambi i casi, la successione converge
ad 1. Se si fosse preso k=0, la successione sarebbe
rimasta stabilmente sullo zero.
Consideriamo ora la funzione ![]() e un valore reale k non nullo. La funzione ha
dominio e immagine coincidenti con i reali non nulli, quindi non
ci sono problemi a costruire una successione per iterazione,
secondo il metodo ormai usuale:
e un valore reale k non nullo. La funzione ha
dominio e immagine coincidenti con i reali non nulli, quindi non
ci sono problemi a costruire una successione per iterazione,
secondo il metodo ormai usuale: 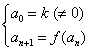 .
.
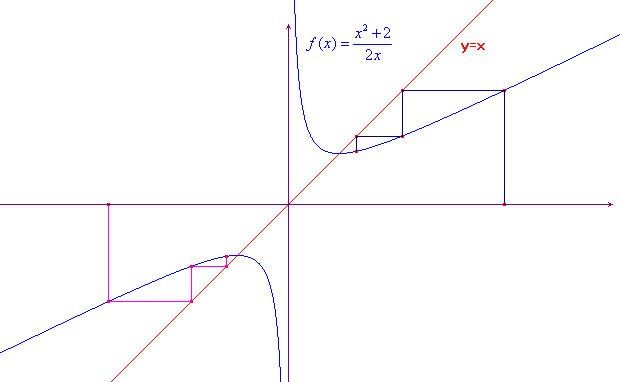
Il grafico qui sopra mostra subito che le orbite costruite a
partire da un k>0 convergono allo stesso punto
(ottenuto per intersezione tra la curva e la bisettrice), di
ascissa (e ordinata!) ![]() ,
tutte quelle costruite a partire da k<0 convergono
a
,
tutte quelle costruite a partire da k<0 convergono
a ![]() .
.
La tecnica considerata in questo esempio è storicamente
molto importante ed era nota, nella sua sostanza, già ai
babilonesi. L'idea che porta alla considerazione di questa
successione si può schematizzare con il ragionamento
seguente. Se a (>0) è un valore approssimato
della radice di 2, si ha: ![]() , ovvero anche
, ovvero anche ![]() è un valore
approssimato della radice di 2. Inoltre
è un valore
approssimato della radice di 2. Inoltre ![]() , ovvero se una delle due approssimazioni è per
difetto, l'altra è per eccesso: prendendo la media
delle due posso sperare di avere un'approssimazione
migliore. La media delle due è
, ovvero se una delle due approssimazioni è per
difetto, l'altra è per eccesso: prendendo la media
delle due posso sperare di avere un'approssimazione
migliore. La media delle due è ![]() , da cui segue la funzione considerata sopra. Il
cosiddetto metodo delle tangenti o di Newton per la risoluzione
numerica di un'equazione fornisce una (tra le possibili)
giustificazioni teoriche a questo ragionamento. Questa tecnica
ricorsiva si presta egregiamente ad essere utilizzata con un
foglio elettronico di calcolo. Puoi vederne un'applicazione
nella calcolo della radice di
due.
, da cui segue la funzione considerata sopra. Il
cosiddetto metodo delle tangenti o di Newton per la risoluzione
numerica di un'equazione fornisce una (tra le possibili)
giustificazioni teoriche a questo ragionamento. Questa tecnica
ricorsiva si presta egregiamente ad essere utilizzata con un
foglio elettronico di calcolo. Puoi vederne un'applicazione
nella calcolo della radice di
due.
Come ulteriore esempio consideriamo la funzione f(x)=cosx. Applicando la tecnica grafica si vede subito che l'orbita di un qualunque punto converge sempre verso l'intersezione tra la funzione coseno e la bisettrice y=x: 0.739085...
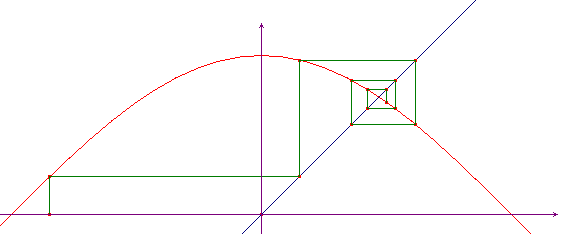
Puoi vedere un calcolo numerico, con foglio elettronico.
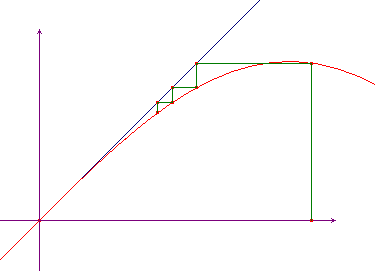 Un
discorso sostanzialmente identico a quello fatto con la funzione
coseno si può fare con la funzione seno, dove si trova
che tutte le orbite convergono a zero, seppure con estrema
lentezza. La lentezza della convergenza, come mostra il grafico
qui a fianco, è legata al fatto che, per x
prossimi a zero, senx si può confondere con
x. Puoi vedere un calcolo
numerico eseguito con foglio elettronico.
Un
discorso sostanzialmente identico a quello fatto con la funzione
coseno si può fare con la funzione seno, dove si trova
che tutte le orbite convergono a zero, seppure con estrema
lentezza. La lentezza della convergenza, come mostra il grafico
qui a fianco, è legata al fatto che, per x
prossimi a zero, senx si può confondere con
x. Puoi vedere un calcolo
numerico eseguito con foglio elettronico.
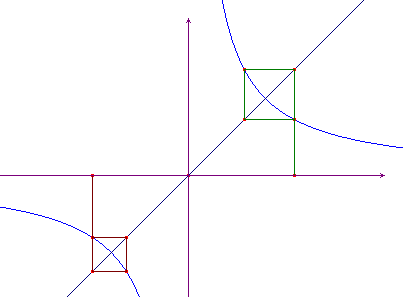 Per
concludere con questi esempi introduttivi consideriamo la
funzione f(x)=1/x. Poiché f(1)=1 ed
f(-1)=-1, si conclude che le orbite di 1 e di -1 sono
costituite solo dai punti 1 e -1 rispettivamente. Se prendiamo
un altro punto k (non nullo) si ha
Per
concludere con questi esempi introduttivi consideriamo la
funzione f(x)=1/x. Poiché f(1)=1 ed
f(-1)=-1, si conclude che le orbite di 1 e di -1 sono
costituite solo dai punti 1 e -1 rispettivamente. Se prendiamo
un altro punto k (non nullo) si ha ![]() , mentre f(f(k)=k. Se ne deduce che le orbite
dei punti diversi da 1 e -1 oscillano continuamente tra
1/k e k.
, mentre f(f(k)=k. Se ne deduce che le orbite
dei punti diversi da 1 e -1 oscillano continuamente tra
1/k e k.