Radici nei complessi: esercizi
Esercizio 1 Risolvere l'equazione z4+1=0
Si tratta di trovare le radici quarte di -1. Intanto si ha -1=[1,π]. Allora
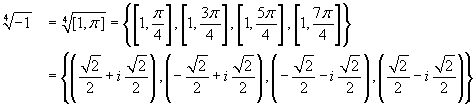
Esercizio 2 Calcolare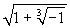 
.
Si ha, intanto,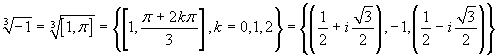 
. Dovremo ora eseguire i seguenti calcoli:
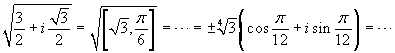
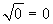
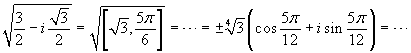
Esercizio 3 Risolvere l'equazione .
Applichiamo la formula risolutiva: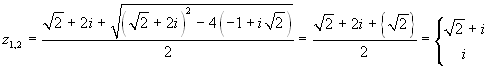 
. Si noti la difficoltà nelle
notazioni, che ci ha portato a scrivere il secondo radicale tra
parentesi graffe: mentre il primo radicale indica la radice di 2
nei reali (e quindi un unico numero!), il secondo indica la
radice di due nei complessi (e quindi un insieme di due numeri).
Bisogna prestare la massima attenzione nei calcoli, per non
incorrere in errori grossolani. Forse le radici nei complessi
andrebbero scritte sempre sotto forma di insieme, usando le
parentesi graffe, ma che complicazioni poi nei calcoli!
Esercizio 4 Sapendo che i è una radice del polinomio z3-4iz2-5z+2 i, trovare le altre due radici.
Si comincia con l'eseguire la divisione del polinomio dato per z-i.
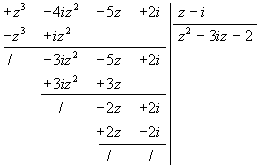
A questo punto basta trovare le due radici di z3-3iz-2, che sono i e 2i.
Esercizio 5 Calcolare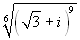 
.
Attenzione a non semplificare l'indice della radice con
l'esponente del radicando: rimarrebbe una radice quadrata,
che ha solo due valori, mentre la radice sesta ne ha sei! Si ha,
intanto,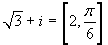 
.
Poi:
Esercizio 5 Si consideri il polinomio z4+z2+1. Si determinino le sue radici e si controlli che esse sono a due a due coniugate. Scomposto il polinomio nella forma (z-z1)(z-z2)(z-z 3)(z-z4), si trasformi questo prodotto nel prodotto di due polinomi di secondo grado a coefficienti reali.
Intanto: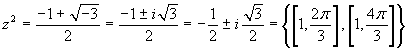 
.
Successivamente si trova:
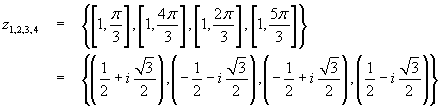
Si vede subito che le radici ottenute sono a due a due coniugate. Se si scompone il polinomio come indicato e si eseguono le moltiplicazioni (z-z1)(z-z4) e (z-z2)(z-z3), si ottiene:
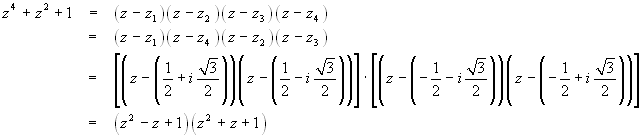
La scomposizione si poteva anche ottenere in maniera immediata osservando che z4+z2+1 = z4+2z2+1-z2 = (z2+1)2-z2 e decomponendo successivamente come differenza di quadrati.
Il risultato di questo esercizio esprime una proprietà generale dei polinomi a coefficienti reali, che si deduce come conseguenza del teorema fondamentale dell'algebra.