Radici nei complessi
Radici n-esime
La formula di De Moivre [ρ,θ]n = [ρn,nθ] permette di dimostrare facilmente il seguente
Teorema: Per ogni numero complesso α = a+ib = [ρ,θ] esistono esattamente n radici n-esime distinte, ovvero n numeri complessi diversi, che indichiamo con z0, z1, ..., zn-1 tali che (zk)n = α. Questi numeri sono dati dalla formula:
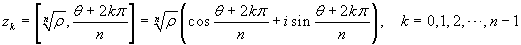
Per la dimostrazione si osservi che, posto z =
[r,φ], si deve avere
[rn,nφ] =
[ρ,θ], ovvero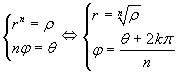 
. Esistono solo n
valori distinti di k che producono angoli distinti (per
la consueta periodicità): si possono scegliere i valori
da 0 ad n-1, come abbiamo fatto sopra e come si fa
d'abitudine.
Osservazioni
Come è noto, nell'insieme dei numeri reali si verifica che:
-
per ogni numero a esiste una ed una sola radice di
indice dispari, ossia uno ed un solo numero reale x
tale che, se n è dispari, xn =
a; questa radice si indica con
;
-
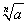per ogni numero reale a>0 esistono due radici
distinte di indice pari, ossia due numeri x tali
che, se n è pari, xn = a;
le due radici sono tra di loro opposte (quindi una positiva e
una negativa) e quella positiva si indica con
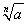, mentre
quella negativa con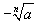 
;
- se a<0, non esiste alcun numero reale x tale che, se n è pari, xn = a;
- se a=0, l'unico numero reale x tale che xn = 0 è 0 stesso (zero ha una sola radice, sia pari che dispari).
In sostanza il simbolo 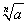indica un unico numero reale e
precisamente l'unica radice di a se n
è dispari (radice che può essere sia positiva che
negativa), mentre indica solo la radice positiva di a
se n è pari. La scrittura nei reali è
facilitata dal fatto che, al massimo, per un numero reale
esistono due radici.
Tutto si complica nei complessi, dove le radici n-esime sono n. Inoltre non essendo possibile definire il concetto di positivo e negativo non è facile stabilire un criterio per privilegiare (almeno nella scrittura) una delle radici sulle altre (nei reali abbiamo privilegiato la positiva sulla negativa e che è interessato può vedere una discussione su questo problema).
Per questo, dato il numero complesso α si
è scelto di indicare con il simbolo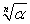 
l'insieme
di tutte le radici n-esime di α. In
sostanza si pone:
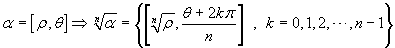
Questa notazione può ingenerare confusione perché
usa un simbolo, che comunemente è adottato per
rappresentare un unico numero, per rappresentare invece un
insieme di n numeri. Alcuni autori hanno introdotto
qualche modifica per evitare questi problemi, per esempio
scrivendo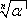 
, ma questo
tipo di simboli non ha avuto fortuna. Non resta che prestare
attenzione: di solito tutto è chiarito dal contesto.
In questo spirito la formula risolutiva per le equazioni di secondo grado si può scrivere in maniera più compatta, evitando il doppio segno davanti alla radice, in quanto il simbolo di radice quadrata indica già (solo nei complessi!) due numeri diversi.
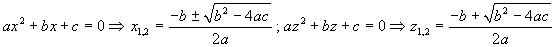
Non è comunque il caso di sottilizzare troppo: in ogni caso anche le radici complesse sono una l'opposta dell'altra (anche se non sono una positiva e una negativa!).
Si noti anche che le usuali proprietà dei radicali in R vanno opportunamente modificate, di solito interpretandole nel senso della teoria degli insiemi. In particolare:
-
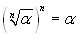(come in R)
-
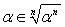(e non 
)
-
-
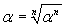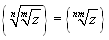
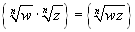
- Non ha senso la scrittura di radice come potenza ad esponente frazionario.
Radici dell'unità
Il caso α = 1 è particolarmente interessante e merita un'analisi particolare.
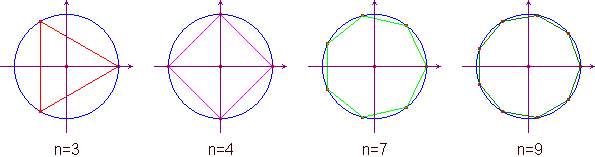
Ora tutte le radici n-esime (qualunque sia n) hanno modulo 1 e quindi nel piano di Gauss si situano sulla circonferenza di centro l'origine e raggio 1. Inoltre, poiché 1n vale ovviamente 1, il numero 1 stesso appartiene all'insieme delle radici n-esime, per ogni n. Se si osserva che gli argomenti delle radici sono, nell'ordine, 0, 2π/n, 3π/n, ..., (n-1)π/n, si conclude subito che esse si situano sui vertici di un poligono regolare di n lati, inscritto nella circonferenza e con un vertice nel punto (1,0). Questa osservazione riconduce il problema del calcolo esplicito delle radici in forma algebrica a quello generale della ciclotomia.
Se consideriamo poi un complesso α qualunque,
potremo scrivere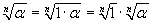 
. Ci sono n radici
n-esime sia di 1 che di α. Si deduce
allora che per trovare le radici di α
basterà trovarne una e poi moltiplicarla per le
n radici n-esime di 1: se costruiamo una
tabella contenente le radici n-esime di 1, ci
sarà molto più facile trovare le radici degli
altri numeri complessi.
Il caso delle radici quadrate
Si tratta di un caso particolarmente importante nelle applicazioni, in quanto legato al problema della risoluzione di equazioni di secondo grado.
Nelle applicazioni, infatti, ha spesso interesse, oltre alla forma trigonometrica di un complesso, anche la forma algebrica. Osserviamo esplicitamente che la formula precedentemente trovata per il calcolo delle radici n-esime, permette un agevole calcolo dell'argomento di qualunque radice n-esima solo se si conosce l'argomento del numero di cui si vuole estrarre la radice. In generale il numero di cui trovare le radici viene dato nella sua forma algebrica, e quindi è possibile ricavare esplicitamente il seno ed il coseno dell'argomento, mentre l'argomento stesso deve venire espresso utilizzando le funzioni inverse arcsin e arccos, tranne alcuni casi favorevoli.
Inoltre, una volta trovati gli argomenti delle radici n-esime, il passaggio alla forma algebrica richiede il calcolo del seno e coseno di questi argomenti, cosa esplicitamente possibile solo in casi favorevoli.
Consideriamo qualche esempio per chiarire il concetto:
-
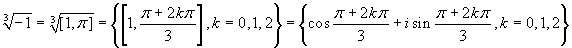e i calcoli indicati nell'ultima parentesi possono essere
agevolmente eseguiti
-
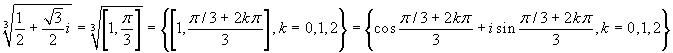e il calcolo tra parentesi non può essere eseguito
mediante radicali quadratici (l'angolo di 60° non
può essere trisecato con riga e compasso!)
-
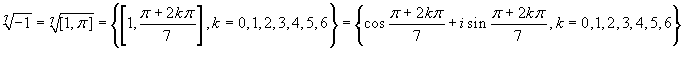e questa volta i calcoli indicati nell'ultima parentesi
non possono essere eseguiti (problema della suddivisione di
un angolo in sette parti)
-
.
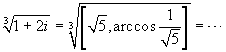Nel caso delle radici quadrate (e in realtà anche delle radici n-esime dove n è una potenza di 2), i calcoli si possono invece sempre eseguire, utilizzando eventualmente le formule di bisezione. Anche in questo caso proponiamo un esempio per chiarire il concetto.
.
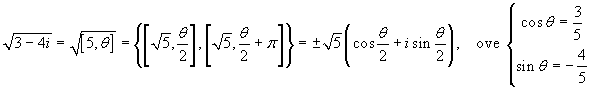Anche se non si riesce ad esprimere l'argomento θ in
termini di angoli notevoli, si possono comunque eseguire i
calcoli indicati con le citate formule di bisezione, osservando
che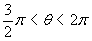 
e quindi 
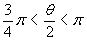. Si trova facilmente:
.
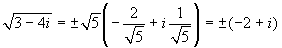Naturalmente il calcolo delle radici quadrate si poteva anche fare senza l'uso della forma trigonometrica, semplicemente osservando che si trattava di calcolare x ed y tali che (x+iy)2 = 3-4i e giungendo ad un sistema di due equazioni in due incognite.