Costruzione di un triangolo dati α, R, 2p
Siano dati l'angolo di vertice A, il raggio del cerchio circoscritto, e il perimetro.
Costruita una circonferenza di raggio R e un angolo alla circonferenza uguale a quello dato, si determina subito la lunghezza del lato a. A questo punto sono noti il semiperimetro p e il segmento p-a.
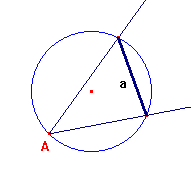
Le circonferenze di vertice A e raggi p-a e p intersecano i lati dell'angolo dato, rispettivamente, in X ed Y e U e V. X ed Y sono i punti di contatto della circonferenza inscritta con i lati AB e AC: la circonferenza si può facilmente costruire. U e V sono i punti di contatto di una circonferenza ex-inscritta con gli stessi lati: anche questa circonferenza si può facilmente costruire.
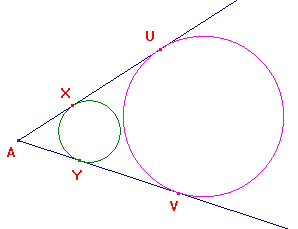
A questo punto basta tirare una tangente comune alle due circonferenze per ottenere il triangolo cercato
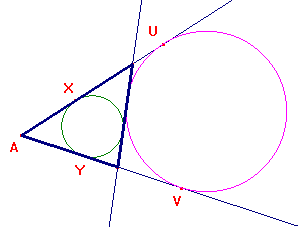
La Cabri costruzione non richiede alcuna particolare attenzione. Muovendo i punti P, R e 2p puoi variare i dati.