L'eptagono regolare
Si tratta di una figura non costruibile con riga e compasso, come prova il teorema di Gauss sui poligoni costruibili. Purtroppo numerosi testi di disegno geometrico propongono costruzioni di questo poligono, senza precisare che devono, necessariamente, essere costruzioni approssimate. É ovvio che, ai fini delle applicazioni, le costruzioni proposte possono essere sufficientemente precise e quindi accettabili, ma sarebbe opportuno precisare che si tratta comunque di costruzioni approssimate. La verifica si può fare agevolmente con un software di geometria dinamica, come Cabri, come si può vedere dalle costruzioni qui sotto riportate.
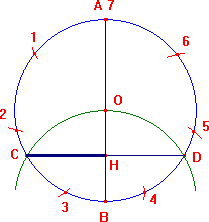
Considerata la circonferenza O, se ne tracci il diametro AB. Con centro in B e apertura BO si individuino i punti C e D. CH è, approssimativamente, il lato dell'eptagono regolare inscritto. Se si riporta il segmento CH, a partire da A, nei punti 1, 2, 3, 4, 5, 6, 7, si constata che il punto 7 non coincide con A, come dovrebbe essere se la costruzione fosse esatta.
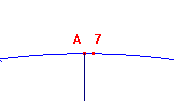
Per una verifica del fatto che la costruzione è approssimata si può ingrandire la circonferenza e zoomare un intorno dei punti A e 7. La figura è riportata qui qui sotto. I pigri possono scaricare la figura fatta con Cabri e provare ad ingrandirla.
Esistono numerose altre costruzioni approssimate, ma quella qui riportata ci è parsa la più semplice ed è più che sufficiente per le normali applicazioni.
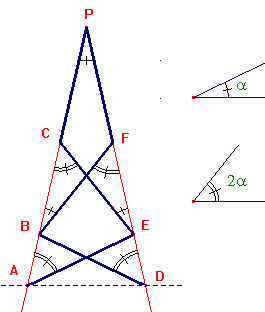
Tra le costruzioni che coinvolgono tecniche diverse da quelle classiche (riga e compasso), ci è particolarmente piaciuta quella proposta da C.Johnson, in Mathematical Gazette, No.407, 1975. Si tratta di disporre 6 stuzzicadenti identici come in figura, in modo che i punti A, B, C, P e D, E, F, P siano allineati: l'angolo in P è allora di π/7. La prova si fa immediatamente se si osserva che gli angoli segnati con una e due linee sono uno doppio dell'altro (triangoli isosceli e proprietà dell'angolo esterno), e si usano le note proprietà della somma degli angoli di un poligono.