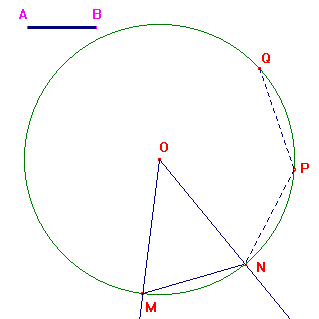
Il problema generale della ciclotomia

Si tratta del problema di dividere una circonferenza in n parti uguali, cioè di costruire un poligono regolare di n lati inscritto nella circonferenza, o, equivalentemente, di costruire un poligono regolare di lato assegnato.

Il problema di sapere quali sono le divisioni possibili con riga e compasso, già affrontato nell'antichità e diffusamente studiato dai Greci, fu definitivamente risolto da Gauss, nel 1796, che giunse alla seguente conclusione:

La formula comprende anche il caso in cui n=2^k. In realtà Gauss provò solo la sufficienza della condizione (all'età di 19 anni!!), mentre la necessità fu provata successivamente da Pierre-Laurent Wantzel nel 1836. I greci conoscevano la costruzione dei poligoni di 3, 4, 5 e 15 lati (oltre a quelli ovviamente che si ottengono raddoppiando questi numeri), ma non riuscirono a trarre conclusioni generali.

La costruzione dei poligoni di tre lati (triangolo equilatero) e di quattro lati (quadrato) è quasi banale. Molto più interessante la costruzione del pentagono, che richiede qualche sforzo di fantasia in più. La costruzione simultanea del pentagono e del triangolo rende poi facile quella del pentadecagono. Dopo queste costruzioni classiche ci vollero duemila anni prima che una nuova costruzione fosse realizzata, appunto da Gauss che indicò quella del poligono di 17 lati  (eptadecagono). Il caso del poligono di 257 lati è stato trattato e risolto da Friedrich Julius Richelot in un articolo dal titolo De resolutione algebraica aequationis x²⁵⁷=1, sive de divisione circuli per bisectionem anguli septies repetitam in partes 257 inter se aequales commentatio coronata, pubblicato sul Crelle's Journal, IX, 1832. Il caso del poligono di 65537 lati è stato trattato e risolto da J.Hermes, dopo oltre dieci anni di lavoro. I risultati, presentati nell'articolo Über die teilung des kreises in 65537 gleiche teile, del Nachr. Königl. Geselsch. Wissench. Gött. Math.-Phys. Klasse (1894),  sono ancora depositati, sotto forma di manoscritto, in una voluminosa scatola della biblioteca dell'Università di Göttingen, dove probabilmente riposeranno per lungo tempo senza destare particolare curiosità da parte degli studiosi: è forse uno dei tanti casi di ricerca matematica difficile, ma sostanzialmente, a nostro avviso, sterile e poco feconda di risultati. Da qualche parte abbiamo addirittura letto il seguente commento, che condividiamo: "What a pointless waste of effort!".

Il teorema di Gauss ha come conseguenza che l'eptagono non è costruibile (è il primo di una lunga serie) e che tutte le costruzioni proposte sui manuali di disegno tecnico sono solo approssimate, anche se di solito non ci sono accenni a questo fatto.

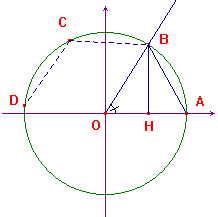
Dal punto di vista analitico è chiaro che il problema della ciclotomia è equivalente a quello di esprimere il seno (o il coseno) dell'angolo 2π/n in termini di radicali quadratici. Se AB è il lato di un poligono regolare di n lati, è chiaro che l'angolo AOB è 2π/n e che la conoscenza di BH (o di OH), cioè del seno (o del coseno) di quest'angolo, rende possibile la costruzione del poligono. Se questo seno (o coseno) é espresso in termini di radicali quadratici, la costruzione è possibile con riga e compasso. Naturalmente si può anche considerare l'angolo di π/n.

Se si lavora nel campo complesso, il problema della ciclotomia è algebricamente equivalente a quello di trovare le radici n-esime dell'unità, cioè di risolvere l'equazione zⁿ - 1 = 0. Poiché, per ogni n, z=1 è una radice l'equazione da risolvere si riduce a .

Costruire un poligono regolare inscritto in una circonferenza è la stessa cosa che costruire un poligono regolare di lato assegnato. Tra le tante costruzioni possibili indichiamo quella più elementare basata sull'uso del teorema di Talete per costruire il quarto proporzionale dopo tre segmenti dati. Per visualizzare la costruzione segui i passi indicati qui sotto.

uno	due	tre