Applicazioni della scrittura decimale
L'applicazione probabilmente più famosa della scrittura decimale dei reali è una semplicissima dimostrazione della non numerabilità dei reali. La prima dimostrazione di questo risultato è stata pubblicata da G.Cantor nel 1874, sul Giornale di Crelle. Nello stesso articolo si dimostrava sia la numerabilità dei razionali che la non numerabilità dei reali: due risultati stupefacenti e che, in sostanza, rendevano pienamente merito a Zenone che, più di duemila anni prima, aveva intuito che molte proprietà di ordine quantitativo degli insiemi infiniti sono notevolmente diverse da quelle degli insiemi finiti. E' infatti dall'applicazione agli insiemi infiniti di proprietà evidenti degli insiemi finiti che derivano, sostanzialmente, i paradossi di Zenone.
Consideriamo, per semplicità, i reali dell'intervallo [0,1[. Se
x è uno
di questi numeri, allora x=0,a1a2...an... e possiamo sempre
pensare che l'allineamento decimale sia proprio. Supponiamo che [0,1[ sia numerabile: allora i
suoi elementi possono essere messi in fila e numerati usando i numeri naturali come indice:
[0,1[={x1,x2,x3,...}, dove ogni xk ha un suo
allineamento decimale, del tipo 
. Consideriamo ora il seguente allineamento decimale
0,b1b2...bn..., ove 
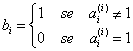, un allineamento decimale costruito quindi in modo da
renderlo diverso da tutti gli allineamenti decimali dei numeri xk. Questo
allineamento corrisponde ad un reale di [0,1[ diverso da tutti gli xk. Ciò
contraddice l'ipotesi che i reali di [0,1[ si potessero numerare usando i naturali come
indice.