Una funzione con tutte le derivate nulle in un punto
Provare che la funzione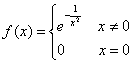 
ha tutte le
derivate nulle nell'origine.
Intanto la funzione è continua come si verifica
facilmente. Cominciamo a calcolare le derivate successive, per
x≠0. Si ha: 
(niente paura, abbiamo semplicemente usato Derive™
per i calcoli!). Si può ipotizzare che le derivate, per
x≠0, abbiano tutte lo stesso aspetto: 
, dove 
è un
polinomio di grado 2n-2. La cosa si può provare
per induzione. Intanto f'(x) è di questo
tipo; se poi f(n)(x) è di questo
tipo, eseguendo la derivazione diretta e semplificando, si
ottiene: 
(abbiamo utilizzato il
fatto che la derivata di un polinomio è sempre un
polinomio di un grado inferiore, oltre alle usuali
proprietà del grado del prodotto di polinomi). É
facile provare (usare la regola di l'Hôpital con il
cambio di variabile 1/x=t)) che 
. Sulla base del teorema sul limite della derivata
possiamo dunque concludere nel senso richiesto.