www.batmath.it

Proprietà locali

Funzioni monotòne in un punto

Una funzione f si dice crescente in un punto c del suo dominio se esiste un intorno di c tale che, nell'intorno,  , mentre . Ovvia la modifica per il concetto di funzione decrescente. Se le disuguaglianze valgono in senso stretto, si parlerà di funzioni strettamente crescenti o strettamente decrescenti. 

A volte, per maggiore sicurezza e considerata la non universalità delle definizioni date, si dice crescente in senso lato al posto di crescente.

É ovvio che una funzione è crescente in un punto se e solo se il rapporto incrementale relativo al punto è positivo in un intorno opportuno del punto: . Questa osservazione è particolarmente utile per le dimostrazioni che seguiranno.

Occorre prestare molta attenzione alla definizione data di funzione crescente in un punto. Spesso si è interessati ad una proprietà molto più raffinata, cioè quella di funzione crescente in un insieme, ovvero di funzione che sale man mano che ci si sposta, nel dominio, da sinistra a destra. Nel caso che qui ci interessa si confronta il valore della funzione in un punto x, vicino ad un punto c, con il valore che la funzione assume nel punto c che è fissato; nel caso della crescenza in un insieme si confrontano i valori che la funzione assume in tutte le coppie di punti dell'insieme. Per rendere chiaro il problema consideriamo un esempio.

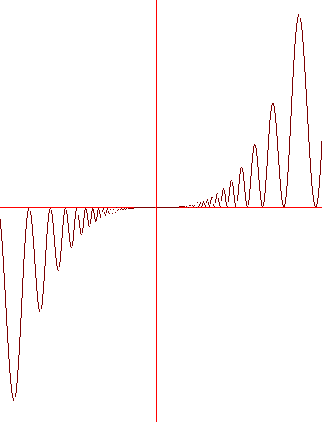
La funzione 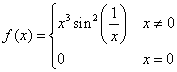è negativa per x<0 e positiva per x>0, dunque è crescente (non strettamente) in 0, ma compie infinite oscillazioni in un qualunque intorno di zero, per cui non è crescente in nessun intervallo contenente zero. Si veda il grafico qui sotto. Si può anche modificare leggermente la funzione per ottenerne una strettamente crescente. Una modifica semplice potrebbe essere 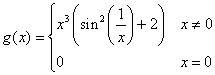, che è sempre compresa tra le due funzioni 2x³ e 3x³. Ne puoi vedere un grafico approssimato.

Per quanto riguarda la crescenza in un punto vale il seguente

Teorema Se la funzione f è derivabile in un punto c del suo dominio con derivata maggiore di zero, allora la funzione è strettamente crescente nel punto.

La dimostrazione di questo risultato è immediata: se la derivata è maggiore di zero, per il teorema della permanenza del segno il rapporto incrementale sarà maggiore di zero in un intorno di c, dal che si deduce la crescenza della funzione.

Si osservi che non è vero il viceversa di questo teorema: la funzione è crescente in 0, ma la sua derivata è nulla. Se però una funzione è crescente in un punto non può avere derivata minore di zero. La modifica per le funzioni decrescenti è immediata.

Massimi e minimi locali (o relativi)

Un punto c si dice punto di massimo locale o relativo per una funzione f, se esiste un intorno di c dove riesce f(x)≤f(c), per ogni x. Il punto si dice di massimo locale stretto (o forte o proprio) se f(x)<f(c), ovviamente per x≠c. Analoga definizione per il minimo.

Quando non si vuole distinguere tra massimo o minimo si parla di estremo locale.

L'aggettivo locale è usato per distinguere questo concetto da quello di minimo o massimo di una funzione nel suo dominio (il minimo o il massimo, se ci sono, dell'insieme immagine); a volte il minimo e il massimo di una funzione nel suo dominio sono chiamati minimo o massimo assoluti.

Vale il seguente

Teorema Se la funzione è derivabile in un punto c, interno al dominio e se la funzione ha in c un estremo locale, allora f'(c)=0.

Limitandoci al caso del massimo, la dimostrazione è immediata: se f'(c) fosse maggiore di zero, la funzione sarebbe crescente in c e quindi, a destra di c, avrebbe valori maggiori di f(c). Analogamente si vede che f'(c) non può essere negativa.

Si noti che è fondamentale che il punto c sia interno al dominio (in pratica che non coincida con gli estremi dell'intervallo di definizione, visto che ci limitiamo a considerare funzioni definite su intervalli). Se per esempio si considera la funzione (semicirconferenza di centro l'origine e raggio 1, situata nel primo e secondo quadrante), agli estremi -1 e 1 si ha un minimo relativo (e anche assoluto), ma la derivata non è affatto nulla.

Si noti altresì che la condizione espressa dal teorema è solo necessaria. La funzione f(x)=x³ ha, in zero, derivata nulla senza avere un estremo locale.

Il problema della ricerca dei massimi e minimi di una funzione è della massima importanza nelle applicazioni e occorre avere una idea precisa delle difficoltà connesse, per questo proporremo ora alcuni esempi, volutamente patologici.

Esempio 1. La funzione ha un massimo locale in x=0, dove non è continua e quindi nemmeno derivabile. Si noti che la funzione è decrescente a sinistra del punto e crescente a destra. Si veda il grafico qui sotto.
 

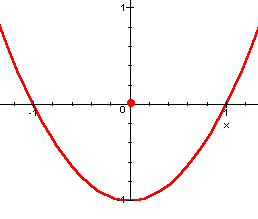
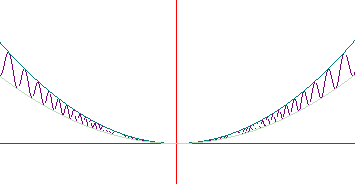
Esempio 2. La funzione 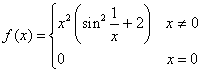, il cui grafico è compreso tra 2x² e 3x², ha in zero un minimo locale forte (che è anche il minimo assoluto della funzione). In questo punto è derivabile (con derivata nulla sulla base del teorema precedente), ma non è decrescente a sinistra e crescente a destra.
 

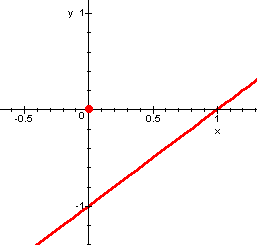
Esempio 3. La funzione ha, in zero, un massimo relativo, ma è crescente sia sulla sinistra che sulla destra del punto zero. Naturalmente, non essendo continua, non è derivabile in zero.

Derivate successive

Per la ricerca degli estremi relativi è spesso utile il seguente

Teorema. Se la funzione f definita in I=]a,b[ è derivabile n volte in I e si ha f'(c)=f''(c)=...=f^(n-1)(c)=0, mentre f⁽ⁿ⁾(c)≠0, allora:

• se n è pari la funzione ha in c un massimo o un minimo relativo a seconda che  f⁽ⁿ⁾(c)<0 oppure 
    f⁽ⁿ⁾(c)>0;
• se  n è dispari la funzione è crescente o decrescente in c a seconda che f⁽ⁿ⁾(c)>0 oppure  f⁽ⁿ⁾(c)<0.

Dimostrazione

Questo teorema (che varrebbe anche in condizioni un po' meno restrittive di quelle qui enunciate) consente di determinare la natura di un punto dove la derivata prima si annulla, senza esaminare la situazione in un intorno del punto, cioè senza controllare che la funzione sia prima crescente e poi decrescente o viceversa. Purtroppo questo teorema non fornisce uno strumento decisivo per la ricerca degli estremi relativi di una funzione, come mostra il successivo esempio 1. In pratica di solito si preferisce studiare il segno della derivata prima in un intorno del punto dove essa si annulla. Esistono però situazioni in cui lo studio di questo segno può essere complesso e allora il teorema appena enunciato può essere di grande aiuto.

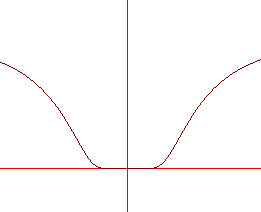
Esempio 1. Si consideri la funzione: 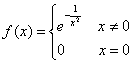. Anche se non è banale, si può provare che tutte le derivate si annullano per x=0, per cui il teorema precedente non è di alcuna utilità. É d'altro canto immediato che f(x)>0 per x≠0, mentre f(0)=0, per cui 0 è un punto di minimo relativo stretto. Il grafico qui sotto mostra il significato di questo risultato in termini di appiattimento del grafico in un intorno dell'origine.

Esempio 2. Trovare i massimi e minimi relativi della funzione . Calcoliamo le derivate prima e seconda (noi abbiamo usato il solito Derive™ per evitare fatiche!):  . Si trova facilmente , , da cui segue che il primo è un punto di minimo, mentre il secondo è di massimo.

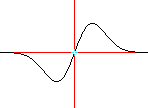
Non sarebbe stato difficile trovare il segno della derivata prima e concludere allo stesso modo. Osserviamo però, in particolare per le applicazioni al calcolo automatico, che il teorema sulle derivate successive consente di ricondurre il problema della ricerca degli estremi relativi al calcolo del segno di una derivata (la seconda nel nostro esempio) in un punto, anziché in un intorno (per la derivata prima) del punto.

copyright 2000 et seq. maddalena falanga & luciano battaia

pagina pubblicata il 01/10/2002 - ultimo aggiornamento il 01/09/2003