Convessità e derivata prima - dimostrazione
Sia f una funzione derivabile due volte in un
intervallo [a,b].
Allora condizione necessaria e sufficiente perché la
funzione sia convessa è che la derivata prima sia
crescente.
Premettiamo alla dimostrazione di questo teorema una utile condizione caratteristica delle funzioni convesse in un intervallo, che deriva immediatamente dalla definizione.
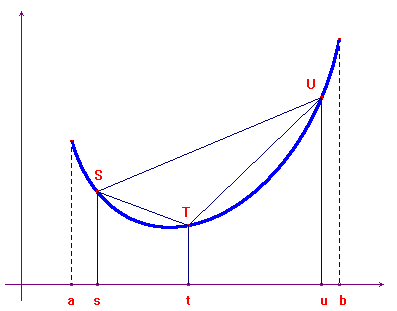
Presi, nell'intervallo [a.b] tre punti s, t, u, nell'ordine e considerati i punti S, T, U corrispondenti sul grafico della funzione, è immediato verificare che la funzione è convessa se, e solo se, il coefficiente angolare della retta SU è compreso tra quello delle rette ST e TU.
In formule la funzione è convessa se e solo se:
.
Supponiamo allora che la nostra funzione sia convessa e
derivabile in [a,b] e consideriamo due punti s ed
u, con s<u. Se t è compreso
tra s ed u, facendo tendere t ad
s nella prima disuguaglianza di sopra e t ad
u nella seconda si trova 
. Ma la funzione è derivabile, e quindi le
derivate destre e sinistre coincidono con le derivate. Questo
basta per provare che la derivata è crescente.
Supponiamo viceversa che la nostra funzione abbia, in [a,b],
derivata crescente e consideriamo, in [a.b], tre punti s, t,
u, nell'ordine. Applichiamo il solito teorema di
Lagrange (sempre lui!) agli intervalli [s,t] e [t,u]: 
, 
, con
s<c<t<d<u. Allora 
. Riducendo allo stesso denominatore, raccogliendo e
riordinando si ottiene 
. Togliendo ad ambo
i membri una prima volta f(s) e una seconda volta
f(u), semplificando e riordinando si ottengono le due
disuguaglianze che caratterizzano la convessità.