Concavità, convessità e flessi
Definizioni
Una funzione definita in un intervallo I si dice convessa se il suo sopragrafico è un insieme convesso. Una definizione equivalente è la seguente: una funzione definita in un intervallo I è convessa se, per ogni coppia di punti c e d dell'intervallo, il segmento che congiunge i punti (c.f(c)) e (d,f(d)) sta sopra il grafico della funzione. A volte per una funzione convessa si usa la locuzione funzione che volge la concavità verso l'alto.
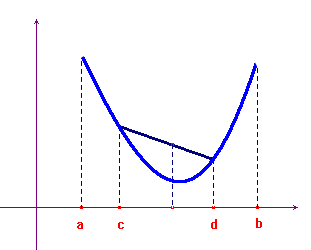
Se il sottografico della funzione è convesso, allora la funzione si dice concava. In questo caso il segmento di cui sopra sta tutto sotto il grafico della funzione. A volte per una funzione concava si usa la locuzione funzione che volge la concavità verso il basso.
La condizione di convessità in un intervallo impone delle condizioni molto restrittive alle funzioni. In particolare si può dimostrare che una funzione convessa in un intervallo:
- è sempre continua in tutti i punti interni;
- ha sempre derivata sinistra e destra finite in tutti i punti interni;
- è addirittura derivabile in tutti i punti interni tranne al più un'infinità numerabile di punti.
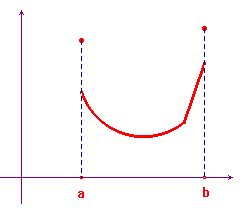
Una funzione convessa può dunque avere discontinuità solo agli estremi dell'intervallo di definizione e può avere, al massimo, un'infinità numerabile di punti angolosi all'interno. La figura qui sotto mostra una funzione convessa discontinua agli estremi dell'intervallo e con un punto angoloso all'interno.
Una funzione convessa gode anche della seguente interessante proprietà: considerato un punto (c,f(c)) del loro grafico, esistono sempre rette per questo punto, tali che il grafico della funzione sta interamente al di sopra di esse. Se la funzione è derivabile in c, l'unica retta con questa proprietà è la tangente. Queste rette si possono dire radenti.
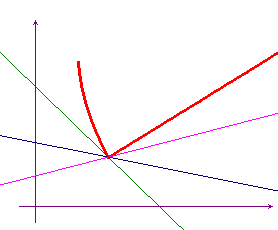
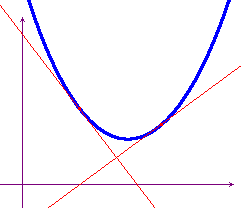
Si può considerare anche una nozione locale di convessità (come abbiamo fatto con la monotonia): una funzione che ammetta tangente in un punto c si dice convessa in c (localmente convessa) se esiste un intorno di c tale che il grafico della funzione, nell'intorno, stia sopra alla tangente. Si possono fornire esempi di funzioni convesse in un punto (i curiosi possono vedere esempi interessanti sulla convessità ), ma non in un intorno del punto, ma non vogliamo essere troppo pignoli.
É importante il fatto che se una funzione è localmente convessa in ogni punto di un intervallo, essa è convessa nell'intervallo. In ogni caso nelle applicazioni allo studio di funzione è importante il concetto di convessità in un intervallo. Abbiamo voluto accennare a questo fatto per invitare il lettore a prestare la massima attenzione alla differenza tra una proprietà locale e una proprietà globale.
Funzioni convesse derivabili
Occupiamoci ora delle funzioni derivabili. Per esse vale il seguente
Teorema. Sia f una funzione derivabile due volte in un intervallo [a,b]. Allora condizione necessaria e sufficiente perché la funzione sia convessa è che la derivata prima sia crescente.
Segnaliamo una conseguenza di questo teorema, molto importante nelle applicazioni:
Teorema. Condizione necessaria e sufficiente
perché una funzione, due volte derivabile in un
intervallo [a,b], sia convessa in [a,b] è che
f''(x)≥0 su tutto l'intervallo.
La dimostrazione, come corollario del teorema precedente, è ovvia. Forniamo comunque una dimostrazione indipendente del fatto che se f''(c)>0, allora la funzione è convessa nel punto c (localmente convessa in c). Analogamente si prova che se f''(c)<0 la funzione è localmente concava in c.
Questo teorema ha una conseguenza ovvia anche sulla ricerca dei massimi e minimi relativi di una funzione:
Se una funzione due volte derivabile ha, in un punto c
interno al dominio, derivata prima nulla e derivata seconda
maggiore di zero, allora ha un minimo locale in
c; se ha derivata prima nulla e derivata seconda minore
di zero ha un massimo locale in c.
Punti di flesso
Si dice punto di flesso o di inflessione per una funzione un punto c interno al suo intervallo di definizione, dove la funzione è derivabile e dove passa da convessa a concava o viceversa. Si noti che questo implica che la funzione attraversa la sua tangente passando da sinistra a destra del punto di flesso.
Anche per il flesso si può dare una definizione locale: un punto si può dire di flesso se la funzione (derivabile) attraversa la sua tangente passando da sinistra a destra del punto. Si potrebbero fornire esempi di funzioni che hanno un flesso in questo senso senza essere "convesse a sinistra e concave a destra" o viceversa, ma non intendiamo essere troppo pignoli. I curiosi possono cercare un esempio di questo tipo tra quelli proposti in qualche altra pagina di questa monografia.
Risulta immediato, da quanto detto sopra, che condizione necessaria per l'esistenza di un flesso in un punto c, per una funzione due volte derivabile, è che f''(c)=0.
Esempi
Esempio 1. La funzione f(x)=x4 ha, per x=0, derivata seconda nulla ma non ha un punto di flesso. Questo prova che la condizione di annullamento della derivata seconda è solo necessaria per l'esistenza di un flesso, ma non sufficiente.
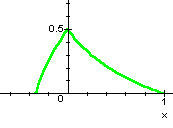
Esempio 2. Una funzione continua può
passare da concava a convessa senza avere un punto di flesso, se
non è derivabile nel punto. Un esempio è fornito
dalla funzione 
, il cui grafico nei
pressi dell'origine è rappresentato qui sotto.
Esempio 3. Determinare gli eventuali punti di flesso per la funzione f(x)=xcos(lnx).
Intanto il dominio della funzione è costituito dai reali
maggiori di zero. Dopodiché la derivata seconda, di cui
dovremo trovare gli zeri e il segno, è: 
. Basta trovare gli zeri e il segno di
cos(lnx)+sin(lnx). Si può utilizzare la
tecnica standard per le funzioni trigonometriche
lineari, ottenendo: 
. Questa è
positiva negli intervalli del tipo 
,
ovvero 
. In questi intervalli la funzione
sarà concava (tenendo conto che -1/x è
negativo). Si tratta di un insieme infinito di intervalli a due
a due disgiunti, situati sulla semiretta delle x
positive, e aventi ampiezza che tende a zero avvicinandosi
all'origine, che tende all'infinito quando ci si
allontana dall'origine. É molto istruttivo provare a
fare un grafico di questa funzione con un programma di grafica
al computer. Tracciato il grafico con le impostazioni
predefinite, si fa uno zoom sui due assi, riducendo o
ingrandendo: le informazioni che si ottengono sono (o meglio
sembrano!) sorprendenti. Puoi vedere il grafico di xcoslnx.
Esempio 4. Provare che una funzione polinomiale di terzo grado ha sempre un unico punto di flesso.
La più generale funzione del tipo indicato è: f(x)=ax3+bx2+cx+d. Poiché f''(x)=6ax+2b, essa cambia di segno nel punto di ascissa x=-b/3a. La funzione passerà dunque da concava a convessa o viceversa e si avrà un flesso.
Derivate successive
Come già per la ricerca degli estremi relativi, anche per la concavità e i flessi spesso è utile il seguente
Teorema. Se la
funzione f definita in I=]a,b[ è derivabile
n volte in I e si ha
f''(c)=...=f(n-1)(c)=0, mentre
f(n)(c)≠0, allora:
- se n è pari la funzione è, in c, concava o convessa a seconda che f(n)(c)<0 oppure f(n)(c)>0;
- se n è dispari la funzione ha, in c, un flesso.
Si possono ripetere, per questo teorema, le considerazioni già fatte a proposito dell'analogo teorema per la ricerca dei massimi e minimi locali.